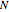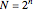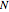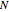Discrete Fourier Transform of Windowing Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
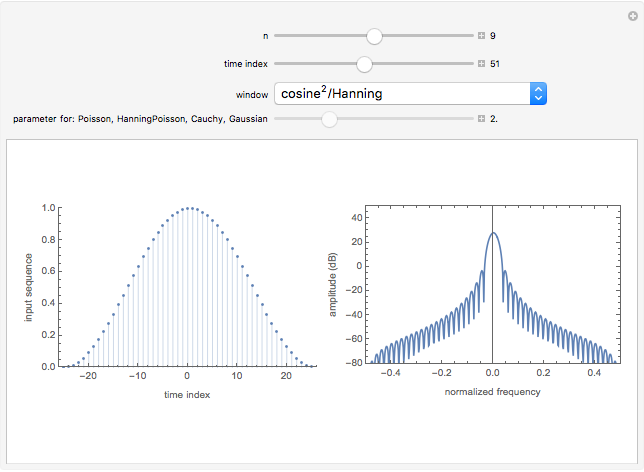
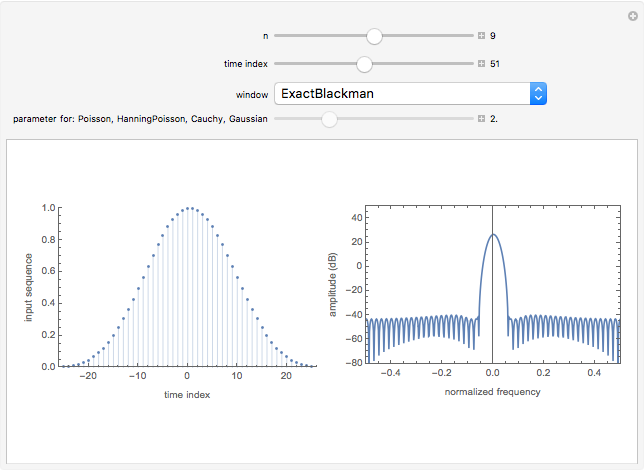
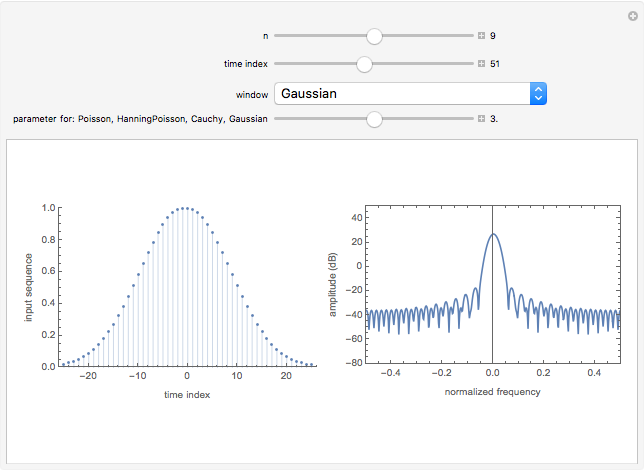
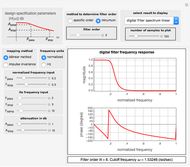
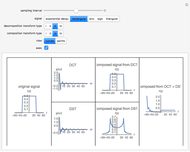
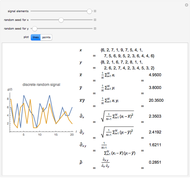
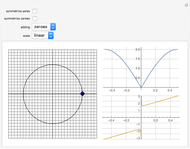
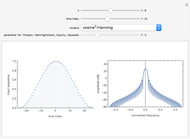
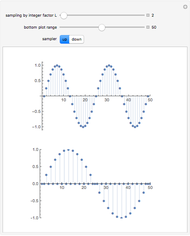
This Demonstration illustrates the frequency domain properties of various windows, which are very useful in signal processing.
[more]
Contributed by: Siva Perla (September 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
F. J. Harris, "On the Use of Windows for Harmonic Analysis with Discrete Fourier Transform," Proceedings of the IEEE, 66(1), 1978 pp. 51–83.
Permanent Citation
"Discrete Fourier Transform of Windowing Functions"
http://demonstrations.wolfram.com/DiscreteFourierTransformOfWindowingFunctions/
Wolfram Demonstrations Project
Published: September 28 2007