Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Drainage of a Hemispherical Tank

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

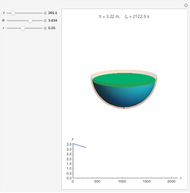
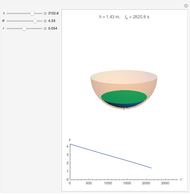
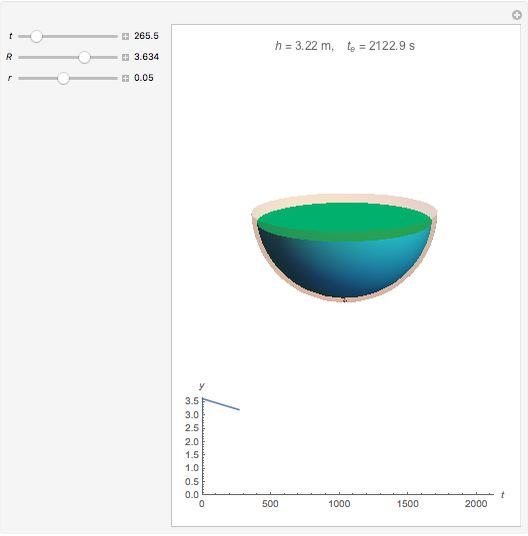
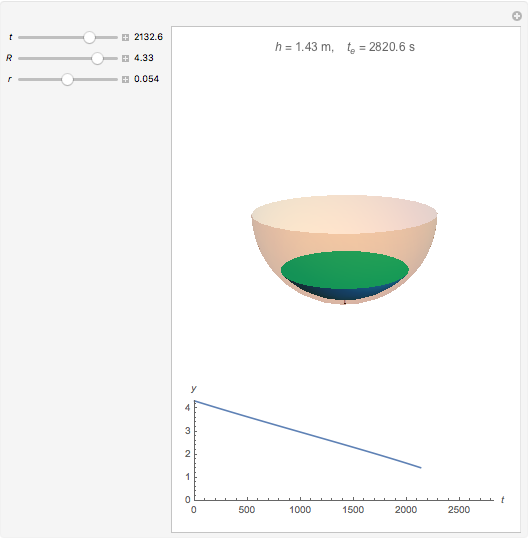
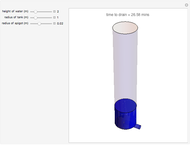
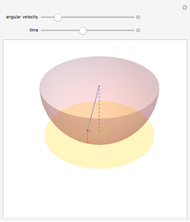
A full hemispherical tank of radius drains under the influence of gravity from a circular hole of radius at the bottom of the tank. The velocity of fluid flowing from the hole is (Torricelli's law), where is the gravitational acceleration and is the height of water at time , which is shown in the tank and plotted below.

Contributed by: Enrique Zeleny (December 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The differential equation for the depth of fluid at time is

.

Integrating and finding the constant yields

.

The time that it takes for the tank to empty is

.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send