Dry Screening Stratification: A Particle Climbing and Settling Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
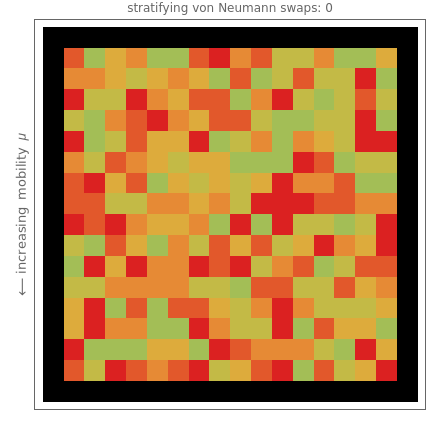
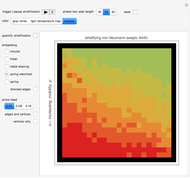
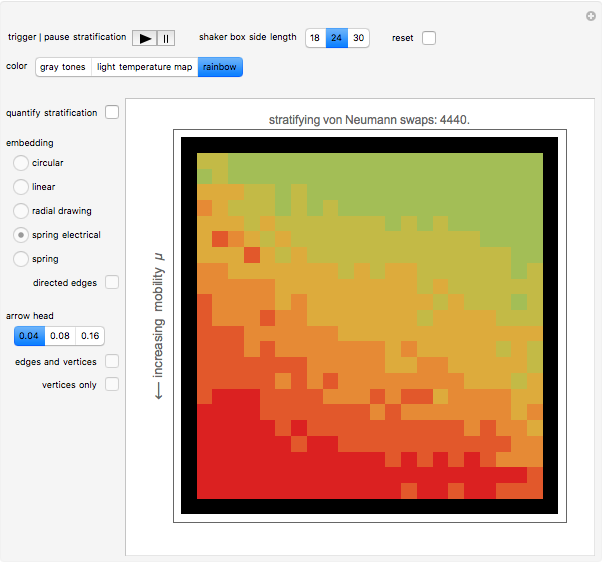
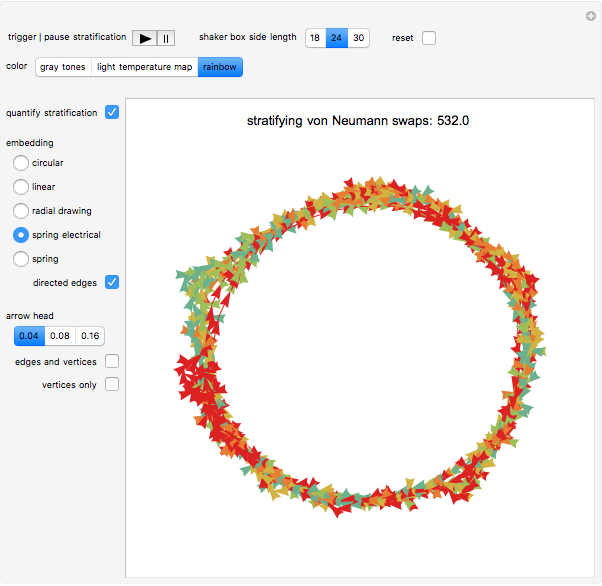
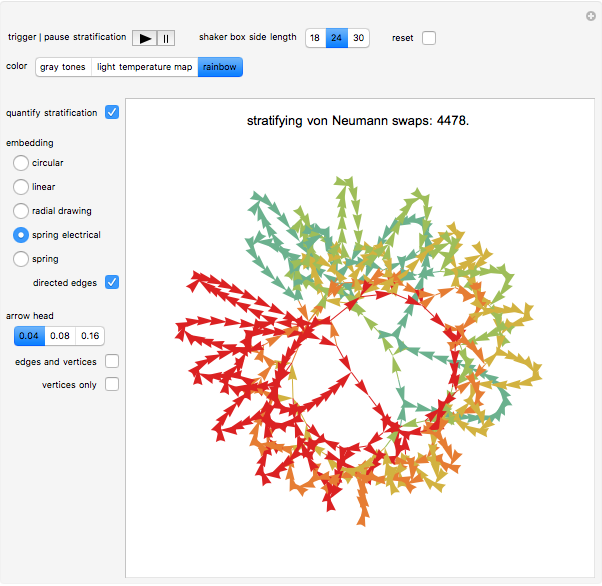
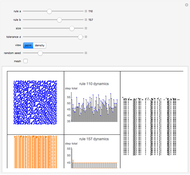
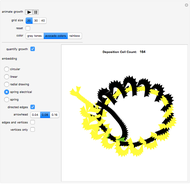
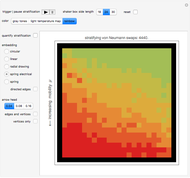
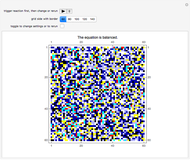
This Demonstration is an idealization of dry screening stratification. The matrix plot shows an end-on view of a black-bordered shaker box that extends into the screen along its border. The box houses ideal cubes of varying mobility  (shown by various colors). The Demonstration shows the climbing and settling nature of the cubes; specifically, the matrix plot simulates the stratification profile that emerges when particles such as these ideal cubes are steadily shaken and then climb and settle under the influence of gravity, while at the same time interacting with one another or with barriers, all under ideal conditions and prevailing linearity. The network view shows a causal relationship in time and 2D space between the cubes; it is further utilized to quantify the matrix plot simulation of the stratification.
(shown by various colors). The Demonstration shows the climbing and settling nature of the cubes; specifically, the matrix plot simulates the stratification profile that emerges when particles such as these ideal cubes are steadily shaken and then climb and settle under the influence of gravity, while at the same time interacting with one another or with barriers, all under ideal conditions and prevailing linearity. The network view shows a causal relationship in time and 2D space between the cubes; it is further utilized to quantify the matrix plot simulation of the stratification.
Contributed by: Michael Dewus (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The control "trigger | pause stratification" triggers the search, update, feedback cellular automaton (SCA); toggle the "reset" control to restart with a new cube arrangement, or check this control to change the shaker box size; uncheck "reset" to restart the stratification.
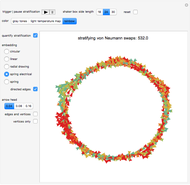
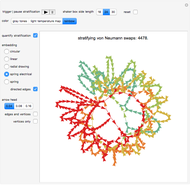
Check the "quantify stratification" control at any time to switch between the matrix plot simulation of the stratification and a network quantification of this simulation. Color information is synchronized between these two views; change the color setting at any time.
With "quantify stratification" checked, check the "directed edges" control to follow the information flow throughout the shaker box (use the "directed edges" control with any of the network embedding methods; linear embedding is informative with both settings of this control). Edge colors are determined by the datum of the vertex a given arrow points to; vertex formats are shown below.
Use the control "edges and vertices" or "vertices only" to get vertex information (please note that "vertices only" has precedence)—pause and mouseover a vertex of interest to locate it in the shaker box. Vertices have this format: {{cube row, cube column}, cube mobility}.
Please see section 3 of the code for more details concerning the controls, and sections 1B and 2 for code functionality.
References
[1] Wikipedia. "Elastic Collision." (Jul 7, 2012) en.wikipedia.org/wiki/Elastic_collision.
[2] Wikipedia. "Mechanical Screening." (Jul 6, 2012) en.wikipedia.org/wiki/Mechanical_screening.
[3] Wikipedia, "Negative Feedback." (Mar 8, 2013)en.wikipedia.org/wiki/Negative_feedback.
[4] Wikipedia, "Positive Feedback." (Mar 8, 2013)en.wikipedia.org/wiki/Positive_feedback.