Magnetization with an Ising Model Based on Q2R Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
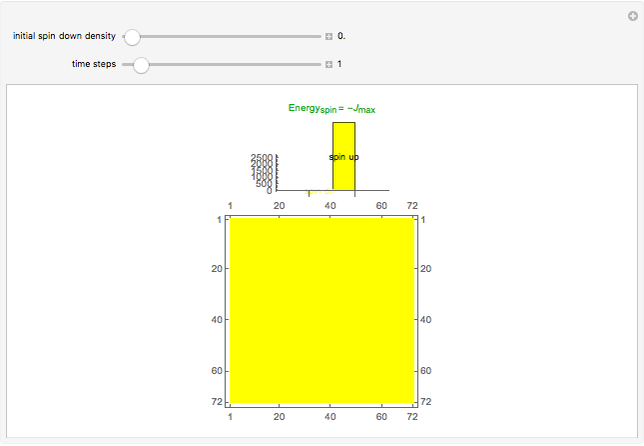
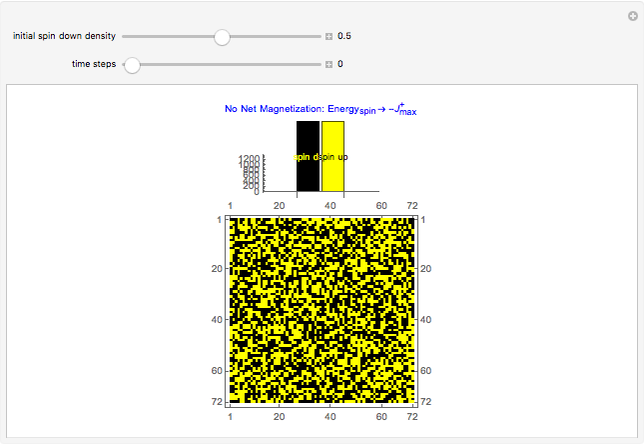
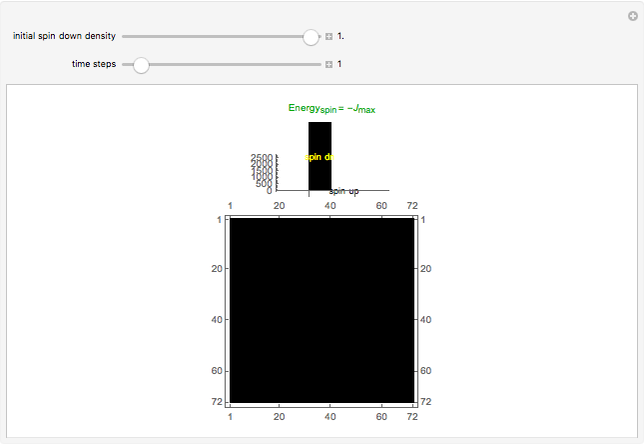
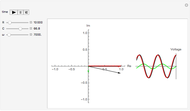
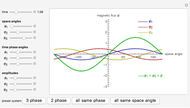
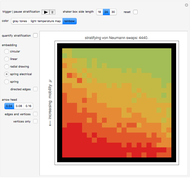
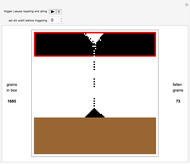
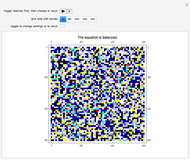
The spontaneous (indigenous, arising from thermal energy stimulus) magnetization of a square atomic lattice comprised of two sub-lattices is tracked by way of its electron spin energy, from full initial spin alignment and maximum negative lattice spin energy, through various phases of magnetization and their spin energies, back to maximum negative spin energy with full initial spin alignment in the opposite direction from that at the beginning. The system achieves magnetization as a function of both the relative initial spin density of the two spins, and time--macroscopic magnetization is observed after an initial transient period, wherein the spin densities, as depicted by the bar-chart, move toward parity for a given relative initial spin density setting greater than ~0.01, or less than ~0.99. The bar-chart quantifies the electron spins relative to the spin down/up domain-level picture of the atomic lattice below it; a textual description of the present state of the system is shown above the bar-chart (a right-pointing arrow in that text means "directed toward"). The degree of disparity between the bars of the bar-chart gives a rough indication of the strength of the intrinsic magnetic field attending the macroscopic magnetization that is realized after the transient period. The computation behind the animation strictly enforces local energy conservation in such a way that spins are only allowed to switch states if doing so introduces no local (automaton neighborhood) energy imbalance, which in turn ensures a minimal energy lattice configuration commensurate with maximum separation of spin-charge and its associated spatial symmetry.
Contributed by: Michael Dewus (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Transitions between the various phases of magnetization indicated above the bar-chart can be understood relative to the rule that controls the automaton—if the configuration of spin states is such that local energy cannot be conserved when applying the rule, then spin states at that instant will not change, and this means that there may or may not be sufficient excess spin states of one type or the other to indicate magnetization. Similarly, a change in spin states may or may not produce sufficient excess spin states of one type or the other to indicate magnetization. The atomic lattice is considered to have a net magnetization when there is an excess of spin states of one type or the other, and when this excess is greater than that spin's initial density. The source code has been liberally commented to offer further programmatic clarity. Experimentally, the various initial spin density configurations would be set by way of either temperature or a given external magnetic field; no external magnetic field is assumed to be applied to the lattice after the initial spin densities are set.
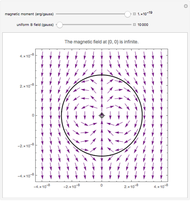
For more information, see the Wikipedia entries for: antiferromagnetism, Curie temperature, diamagnetism, exchange interaction, ferromagnetism, ferrimagnetism, Ising model, magnetic moment, magnetism, Neel temperature, and paramagnetism.
Reference
[1] B. Chopard and M. Droz, Cellular Automata Modeling of Physical Systems, Cambridge: Cambridge University Press, 2005.