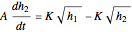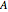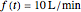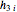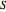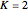,
,
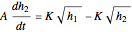 ,
,
 ,
,
where 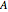 is the cross-sectional area of a tank and
is the cross-sectional area of a tank and  is related to the discharge coefficient for the exit pipes.
is related to the discharge coefficient for the exit pipes.
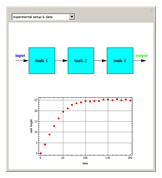
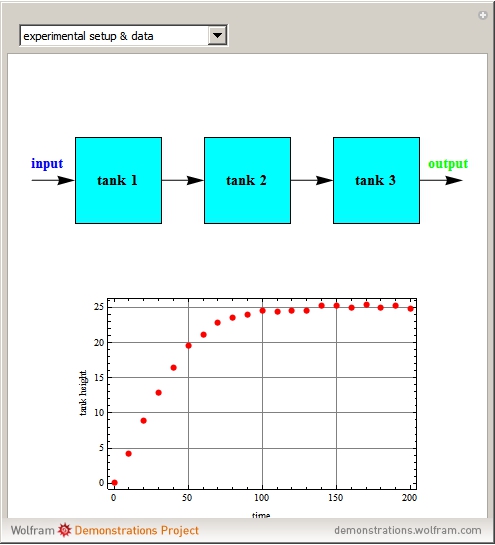
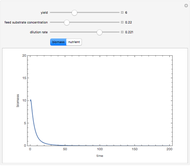
Suppose the height of tank 3 is sampled for a given input function 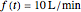 to give the following data list:
to give the following data list:  .
.
Then the constants 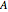 and
and  can be estimated using a least-squares optimization method. That is, we define the following objective function
can be estimated using a least-squares optimization method. That is, we define the following objective function
 .
.
Here  is the height in tank 3 predicted by the model at time
is the height in tank 3 predicted by the model at time  , and
, and 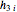 is the value of
is the value of 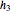 measured at time
measured at time  . The goal then is to determine
. The goal then is to determine 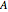 and
and  such that sum of squares
such that sum of squares 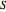 is minimized for
is minimized for  spanning the duration of the experiment.
spanning the duration of the experiment.
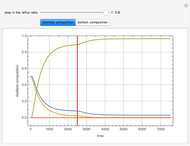
One finds as shown in the second snapshot 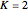 and
and  . It is possible then to solve the governing equations shown above and determine the height of tanks 1 and 2. The second snapshot presents the height versus time for tanks 1, 2, and 3 in blue, magenta, and brown, respectively.
. It is possible then to solve the governing equations shown above and determine the height of tanks 1 and 2. The second snapshot presents the height versus time for tanks 1, 2, and 3 in blue, magenta, and brown, respectively.
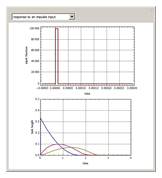
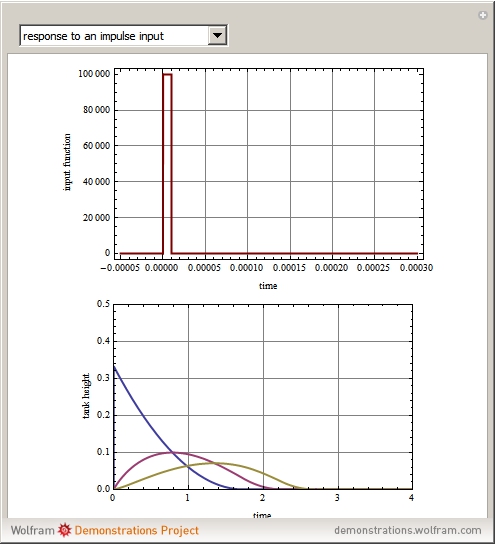
Once 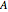 and
and  have been determined, one can run simulations for various forms of the input function: impulse input, triangle input, square input, and staircase input. The subsequent snapshots show the responses for all the above mentioned special input functions, which are shown in red in a separate plot.
have been determined, one can run simulations for various forms of the input function: impulse input, triangle input, square input, and staircase input. The subsequent snapshots show the responses for all the above mentioned special input functions, which are shown in red in a separate plot.
[less]

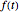 . The heights of the liquid in the three tanks (i.e.
. The heights of the liquid in the three tanks (i.e.  ,
,  ,
, 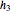 ) obey the following equations:
) obey the following equations: