Energy Density of a Magnetic Dipole

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
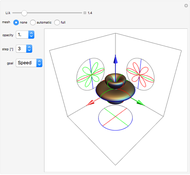
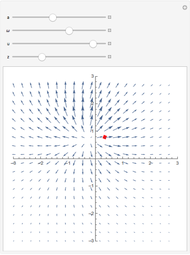
A circular conductor with the current 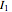 and the radius
and the radius 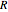 lies in the
lies in the 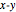 plane at
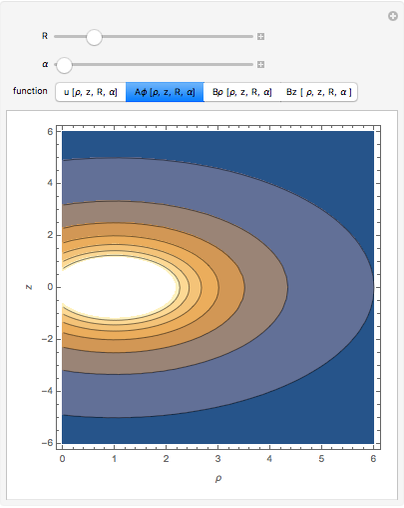
plane at 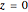 . The vector potential
. The vector potential 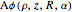 in the
in the  direction as a function of
direction as a function of  and
and  has the same symmetry as the current density in cylindrical coordinates
has the same symmetry as the current density in cylindrical coordinates  ,
,  ,
,  . According to the cylindrical symmetry the observation points in the
. According to the cylindrical symmetry the observation points in the 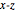 plane can be taken at
plane can be taken at 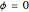 . The source is described by the angle
. The source is described by the angle  , running from
, running from  to
to 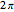 . The following computations are made:
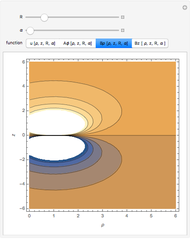
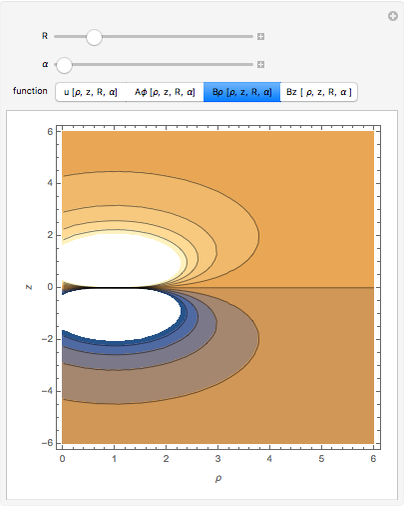
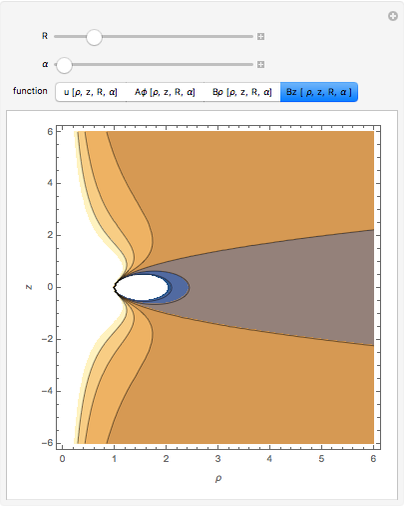
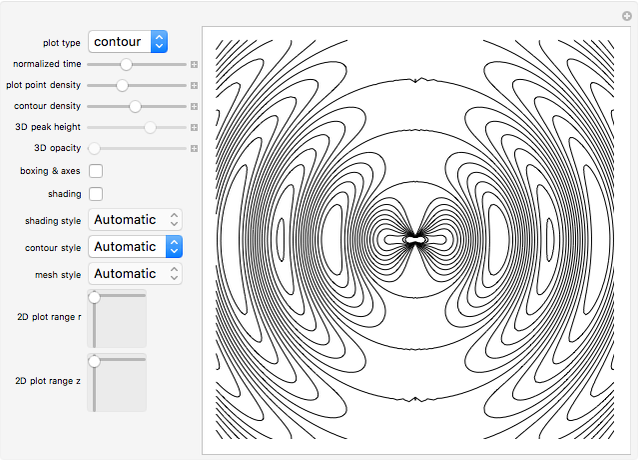
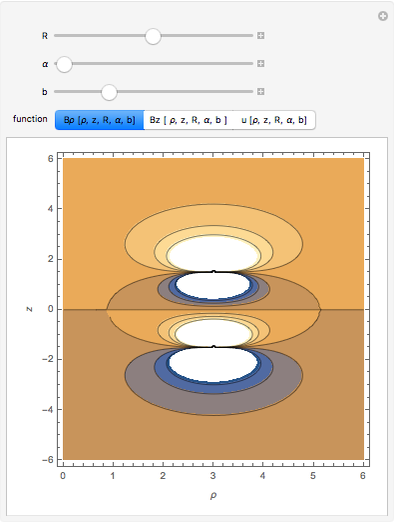
• the magnetic field
. The following computations are made:
• the magnetic field  in the
in the  direction
• the magnetic field
direction
• the magnetic field  in the
in the  direction
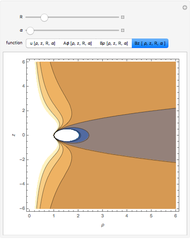
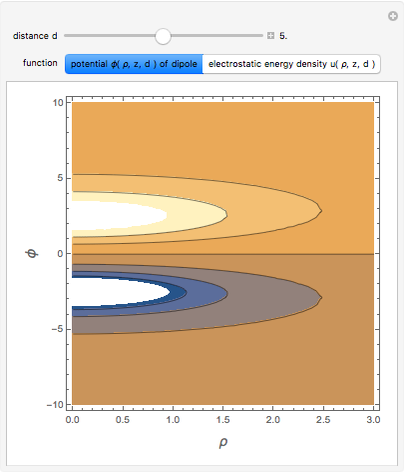
• the magnetic energy density
direction
• the magnetic energy density 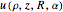 • the integrated magnetic field
• the integrated magnetic field 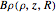 in the
in the  direction
• the integrated magnetic field
direction
• the integrated magnetic field 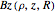 in the
in the  direction
• the integrated magnetic energy density
direction
• the integrated magnetic energy density 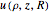 • the integrated vector potential
• the integrated vector potential 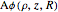 in the
in the  direction
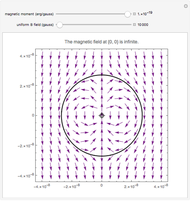
The fields at
direction
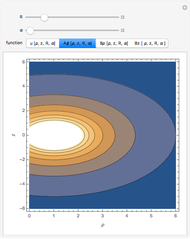
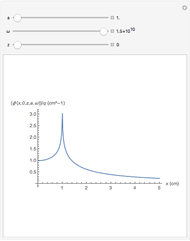
The fields at  can be regarded as a good approximation of the integrated fields. The four field
can be regarded as a good approximation of the integrated fields. The four field 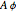 ,
, 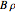 ,
, 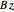 ,
,  are displayed for the four independent variables
are displayed for the four independent variables  ,
,  ,
, 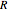 ,
,  . The observation points are described by
. The observation points are described by  ,
,  and the source by
and the source by 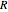 ,
,  .
.
Contributed by: Franz Krafft (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Energy Density of a Magnetic Dipole"
http://demonstrations.wolfram.com/EnergyDensityOfAMagneticDipole/
Wolfram Demonstrations Project
Published: March 7 2011