Fano Resonance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
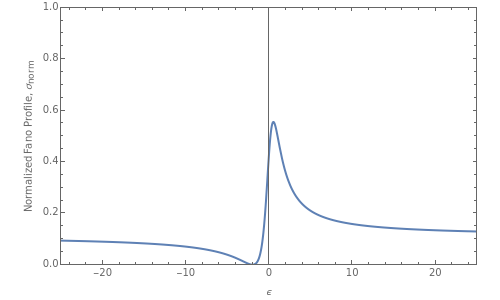
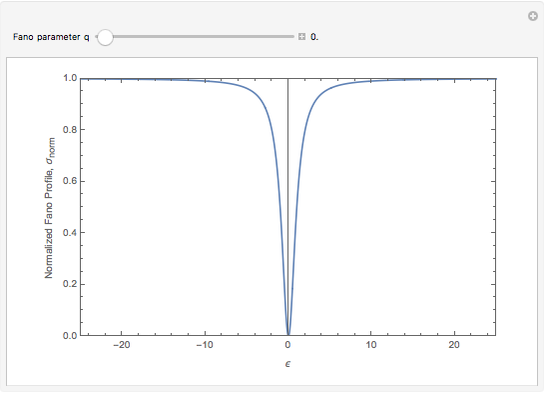
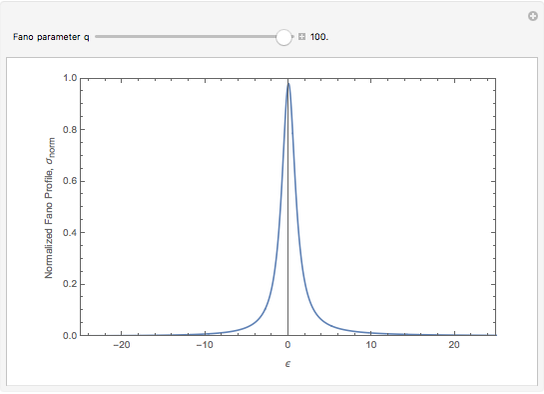
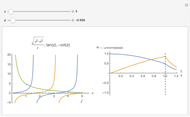
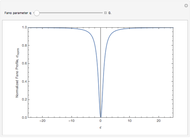
This Demonstration shows the normalized Fano resonance profile, 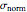 , as a function of reduced energy,
, as a function of reduced energy,  . The phenomenological shape parameter,
. The phenomenological shape parameter,  , alters the asymmetry of the resonance shape. In this Demonstration,
, alters the asymmetry of the resonance shape. In this Demonstration,  values are limited to lie between 0 to 100.
values are limited to lie between 0 to 100.
Contributed by: Shahrul Kadri (March 2011)
(Hokkaido University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A Fano resonance (based on the work of Ugo Fano in 1961) exhibits an asymmetric profile due to interference between the resonant and background scattering probabilities.
The scattering cross section of the so-called Fano profile can be expressed as
 ,
,
where  is a phenomenological shape parameter and
is a phenomenological shape parameter and  is a reduced energy, defined by
is a reduced energy, defined by  ;
; 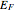 is a resonant energy, and
is a resonant energy, and  is the width of the resonance.
is the width of the resonance.
For comparison between various values of  , the normalized value of the Fano profile is defined by dividing by
, the normalized value of the Fano profile is defined by dividing by 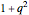 :
:
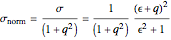 .
.
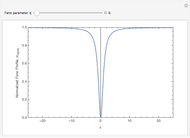
There are three special cases of resonance profiles:
 : Antiresonance characteristic where a dip trough appears at the center of the resonance.
: Antiresonance characteristic where a dip trough appears at the center of the resonance.
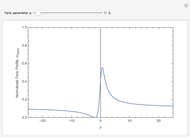
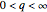 : Asymmetric resonance with maximum peak and minimum trough.
: Asymmetric resonance with maximum peak and minimum trough.
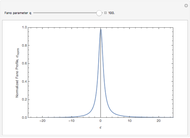
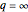 : Lorentzian shape resonance, which is typically seen in oscillating systems.
: Lorentzian shape resonance, which is typically seen in oscillating systems.
References
[1] U. Fano,"Effects of Configuration Interaction on Intensities and Phase Shift," Physical Review, 124(6), 1961 pp. 1866–1878.
[2] Wikipedia, "Fano Resonance," http://en.wikipedia.org/wiki/Fano_resonance.
Permanent Citation