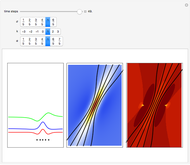
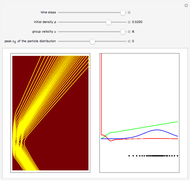
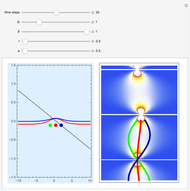
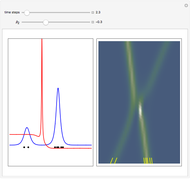
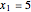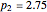The Resonant Nonlinear Schrödinger Equation in the Causal Interpretation of Quantum Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
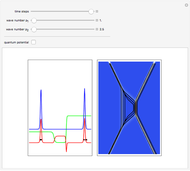
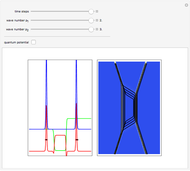
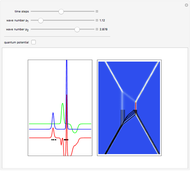
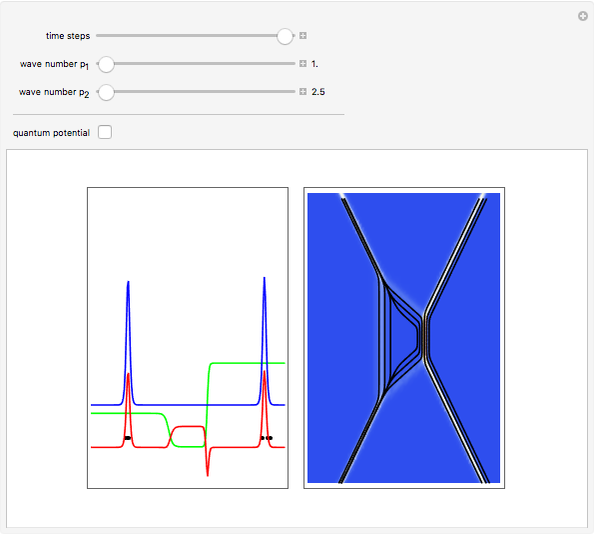
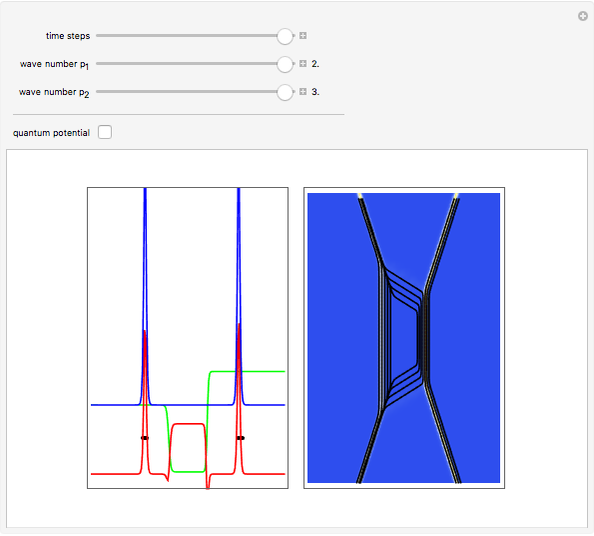
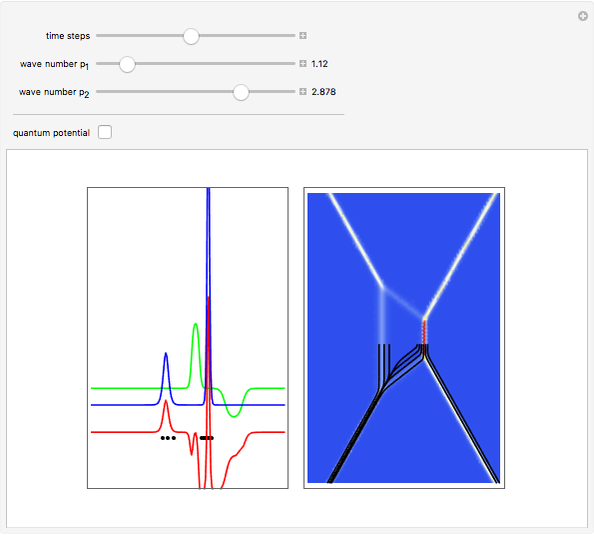
An integrable version of the Resonant Nonlinear Schrödinger equation (RNLS) in 1+1 dimensions admits soliton solutions with a rich scattering structure. The RNLS equation can be interpreted as a particular realization of the nonlinear-Schrödinger-soliton propagating in a so-called "quantum potential". Recently, the RNLS was proposed to describe uniaxial waves in a cold collisionless plasma.
[more]
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Explicitly, the RNLS can be written: 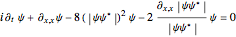 , with
, with 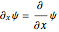 . The nonlinear potential
. The nonlinear potential 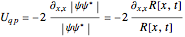 , which could be considered a quantum potential, was first introduced by de Broglie and later by Bohm in a hidden-variable theory (later called a causal interpretation by Bohm) for quantum mechanics. This potential influences, in addition to the external force, the motion of the particles, independently of its intensity. Here, the quantum potential changes the dispersion of the soliton, because when
, which could be considered a quantum potential, was first introduced by de Broglie and later by Bohm in a hidden-variable theory (later called a causal interpretation by Bohm) for quantum mechanics. This potential influences, in addition to the external force, the motion of the particles, independently of its intensity. Here, the quantum potential changes the dispersion of the soliton, because when 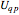 becomes zero, the RNLS changes to the so-called defocusing NLS, admitting a "dark" soliton solution with nonvanishing boundary values. The quantum potential depends only on the form of the wave and in some cases does not fall off with distance.
becomes zero, the RNLS changes to the so-called defocusing NLS, admitting a "dark" soliton solution with nonvanishing boundary values. The quantum potential depends only on the form of the wave and in some cases does not fall off with distance.
By expressing the wavefunction in eikonal form  with
with 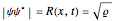 (
( = particle number density), the RNLS equation reduces to two nonlinear partial differential equations, in which
= particle number density), the RNLS equation reduces to two nonlinear partial differential equations, in which 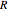 is the real-valued amplitude and
is the real-valued amplitude and 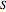 is the real-valued phase of the wavefunction,
is the real-valued phase of the wavefunction,
 ,
,
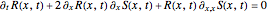 ,
,
where the last term could be simplified, by multiplication of the above equation by 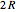 , to the continuity equation
, to the continuity equation
 ,
,
with velocity 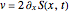 and particle density
and particle density  .
.
The comparison of the RNLS equation with the linear Schrödinger equation (LSE) shows that the nonlinear terms of the RNLS could be regarded as a special form of a potential  in the LSE. In this case, only the gradient of the phase affects the velocity of the single quantum particle, because of the continuity equation for the particle density.
in the LSE. In this case, only the gradient of the phase affects the velocity of the single quantum particle, because of the continuity equation for the particle density.
The analytical solution of the RNLS equation for a two-soliton is:
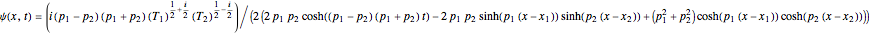
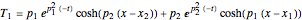 and
and
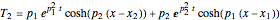 ,
,
where  ,
, 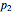 are the wave numbers and
are the wave numbers and 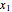 ,
, 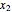 are the initial positions of the maximum density. The system is time-reversible.
are the initial positions of the maximum density. The system is time-reversible.
References
[1] O. K. Pashaev and J.-H. Lee, "Resonance Solitons as Black Holes in Madelung Fluid," Modern Physics Letters A 17(24), 2002 pp. 1601–1619. doi .10.1142/S0217732302007995.
[2] P. R. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.
Permanent Citation