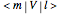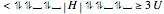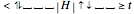Hubbard Model Interactive Calculator for 1D Systems

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
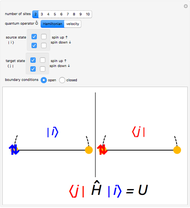
This Demonstration shows the basics of the fermion Hubbard model applied to one-dimensional systems such as chains with 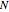 sites with either open or closed boundary conditions and any phase
sites with either open or closed boundary conditions and any phase  at the ends. The Hubbard model provides a very simple but physically powerful description of electronic many-body effects in quantum mechanical systems. This can be understood by considering the form of its Hamiltonian, expressed in second quantization formalism:
at the ends. The Hubbard model provides a very simple but physically powerful description of electronic many-body effects in quantum mechanical systems. This can be understood by considering the form of its Hamiltonian, expressed in second quantization formalism:  , where
, where  and
and  are site indices,
are site indices,  are all pairs of first nearest neighbors sites,
are all pairs of first nearest neighbors sites,  gives the number of electrons on site
gives the number of electrons on site  with spin
with spin  ,
,  and
and  are electron creation and annihilation operators, respectively, and
are electron creation and annihilation operators, respectively, and  and
and 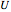 are positive interaction constants, respectively. The
are positive interaction constants, respectively. The  term is a single-particle (tight-binding) term (thus it contains no many-body features) and describes the hopping of electrons localized on atomic-like orbitals between nearest neighbor sites and models the kinetic energy of the system. The
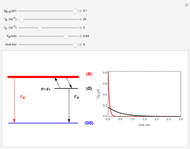
term is a single-particle (tight-binding) term (thus it contains no many-body features) and describes the hopping of electrons localized on atomic-like orbitals between nearest neighbor sites and models the kinetic energy of the system. The  term gives a potential energy contribution to the Hamiltonian and models the Coulomb repulsion between two electrons with opposite spin in the same orbital, hence it is the effective many-body (two-body) term. Another related operator is the velocity operator
term gives a potential energy contribution to the Hamiltonian and models the Coulomb repulsion between two electrons with opposite spin in the same orbital, hence it is the effective many-body (two-body) term. Another related operator is the velocity operator 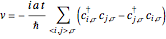 , where
, where  is the lattice parameter of the chain and
is the lattice parameter of the chain and  is the Planck constant (since these are normalization constants, they have been set equal to 1 in the program). The term
is the Planck constant (since these are normalization constants, they have been set equal to 1 in the program). The term 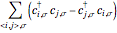 represents the current operator, which is relevant for investigating optical conductivity properties.
represents the current operator, which is relevant for investigating optical conductivity properties.
Contributed by: Jessica Alfonsi (University of Padova, Italy) (March 2011)
Open content licensed under CC BY-NC-SA
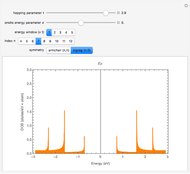
Snapshots
Details
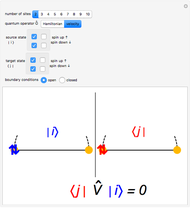
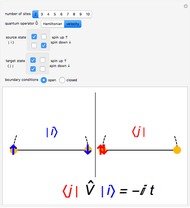
Snapshot 1: Hamiltonian matrix element between two equal states with one doubly occupied site
Snapshot 2: velocity matrix element between a doubly occupied state and a state with one electron on each site
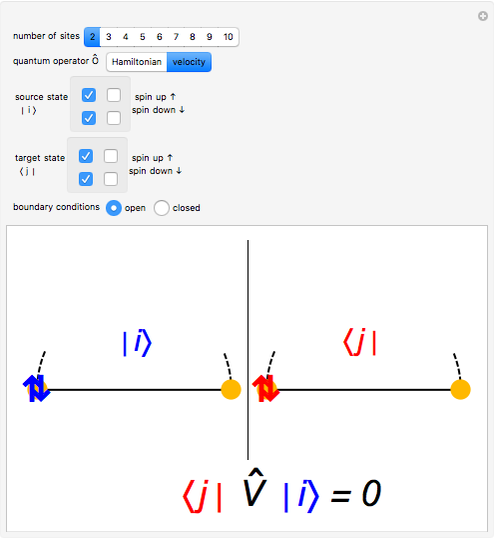
Snapshot 3: velocity matrix element between two equal states with one doubly occupied site
Part of the initialization is taken from the following book: W. Kinzel and G. Reents, Physics by Computer: Programming Physical Problems Using Mathematica and C, New York: Springer, 1998.
H. Q. Lin and J. E. Gubernatis, "Exact Diagonalization Method for Quantum Systems," Computers in Physics 7(4), 1993 p. 400.
J. Alfonsi, "Small Crystal Models for the Electronic Properties of Carbon Nanotubes," Ph.D. thesis, University of Padova, 2009, Chapter 6 and references therein.
Permanent Citation