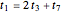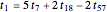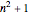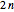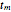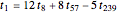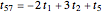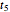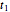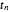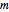Find a Formula for Pi
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
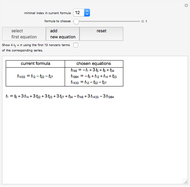
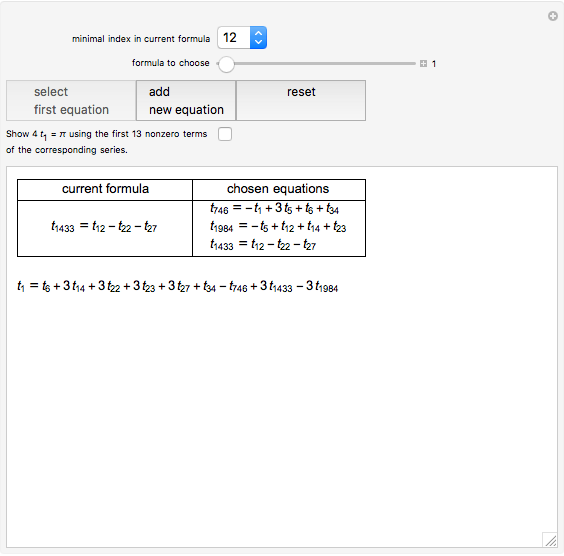
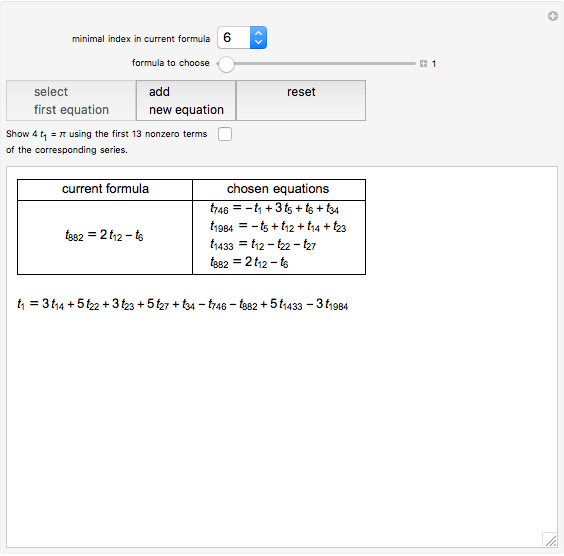
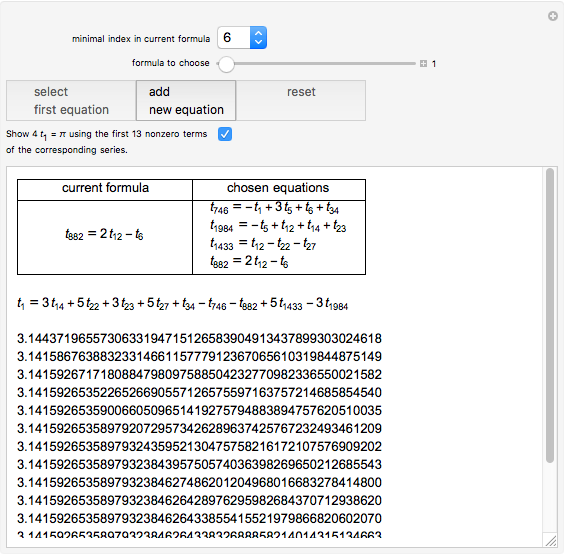
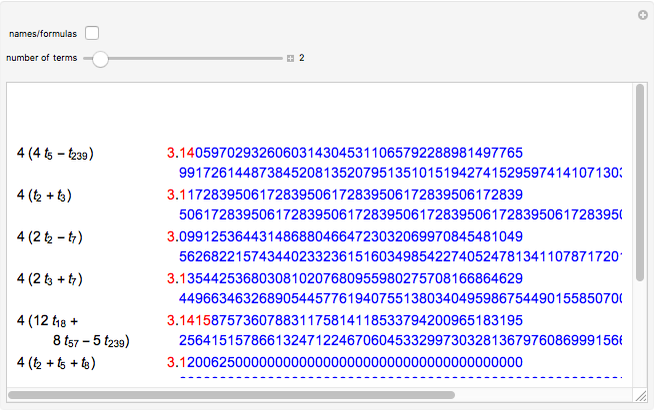
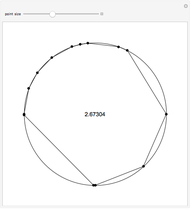
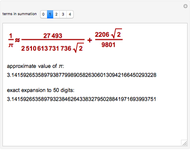
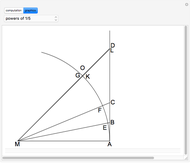
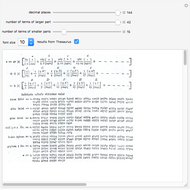
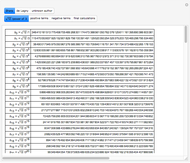
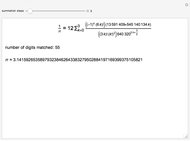
A Gregory number is a number 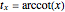 , where
, where  is an integer or rational number. Expanding,
is an integer or rational number. Expanding, 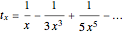 . With
. With 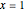 , we get Leibniz's formula for
, we get Leibniz's formula for 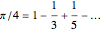 , which converges too slowly. The larger
, which converges too slowly. The larger  is, the better the approximation.
is, the better the approximation.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
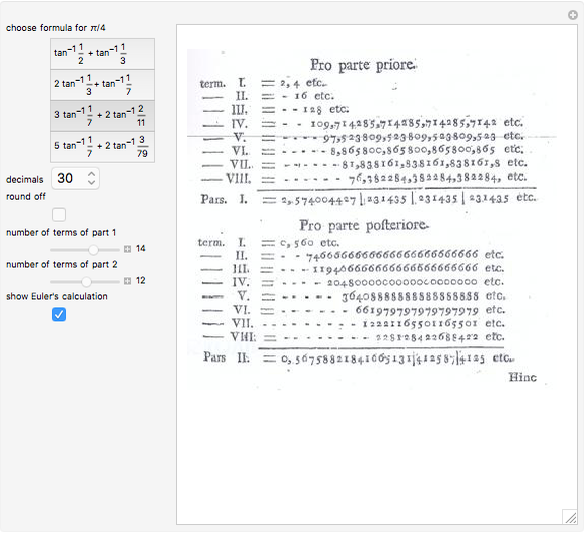
J. H. Conway and R. K. Guy, The Book of Numbers, New York: Copernicus Books/Springer, 2006 pp. 242–247.
Permanent Citation