Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fluids in the Critical Region

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

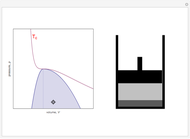
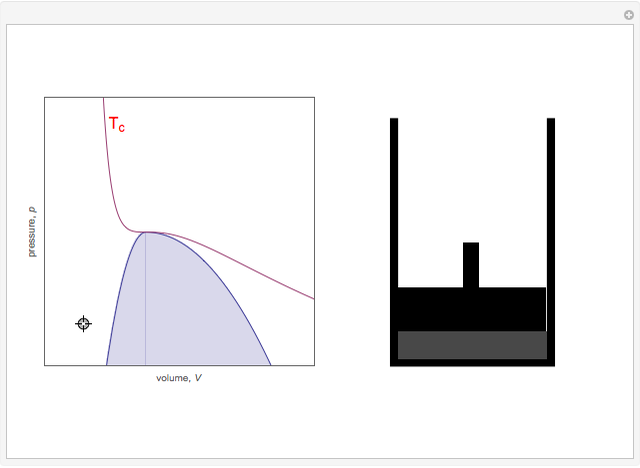
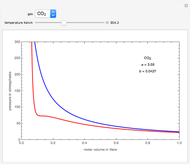
On the left is a phase diagram of the critical region of a representative fluid. Within the shaded area, the fluid separates into two phases: liquid and gas. The critical isotherm is also shown, labeled by the critical temperature 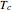. At the critical point, this isotherm is tangent to the two-phase region. A gas can be liquefied only after it is cooled below its critical temperature.

[more]

Drag the locator to vary the pressure and volume of the fluid within the cylinder shown on the right. Within the shaded region, you will see separation into liquid and gaseous phases. The density of a fluid is indicated by its gray-level intensity. Within the two-phase region, the properties of the two phases merge as the critical point is approached.

[less]

Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: This state would be identified as a liquid at a given pressure.

Snapshot 2: At a much higher temperature, the system would be a gas at the same pressure.

Snapshot 3: Going from state 1 to state 2 at constant pressure, the system would go through the two-phase region.

Snapshot 4: An alternative way to go from state 1 to state 2 would be to follow a path around the critical point. The same final state would then be attained continuously, without any phase separation. This is known as the principle of continuity of states.

Snapshot 5: As the critical point is approached, the densities of the two phases approach one another.

Snapshot 6: The densities become equal at the critical point.

Reference: S. M Blinder, Advanced Physical Chemistry; A Survey of Modern Theoretical Principles, New York: Macmillan, 1969 p. 134.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send