Energy Levels of a Morse Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
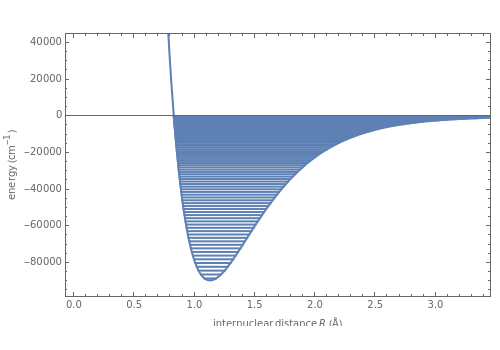
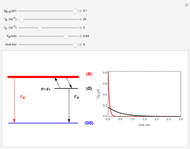
The Morse function 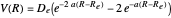 , where
, where 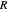 is the internuclear distance, provides a useful approximation for the potential energy of a diatomic molecule. It is superior to the harmonic oscillator model in that it can account for anharmonicity and bond dissociation. The relevant experimental parameters are the dissociation energy
is the internuclear distance, provides a useful approximation for the potential energy of a diatomic molecule. It is superior to the harmonic oscillator model in that it can account for anharmonicity and bond dissociation. The relevant experimental parameters are the dissociation energy 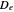 and the fundamental vibrational frequency
and the fundamental vibrational frequency 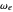 , both conventionally expressed in wavenumbers (
, both conventionally expressed in wavenumbers (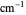 ), the equilibrium internuclear distance
), the equilibrium internuclear distance 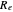 in Angstrom units (Å), and the reduced mass
in Angstrom units (Å), and the reduced mass 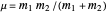 in atomic mass units (amu). The exponential parameter is given by
in atomic mass units (amu). The exponential parameter is given by  in appropriate units. The Schrödinger equation for the Morse oscillator is exactly solvable, giving the vibrational eigenvalues
in appropriate units. The Schrödinger equation for the Morse oscillator is exactly solvable, giving the vibrational eigenvalues  InlineMath, for
InlineMath, for 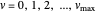 . Unlike the harmonic oscillator, the Morse potential has a finite number of bound vibrational levels with
. Unlike the harmonic oscillator, the Morse potential has a finite number of bound vibrational levels with 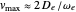 .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
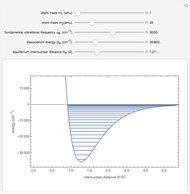
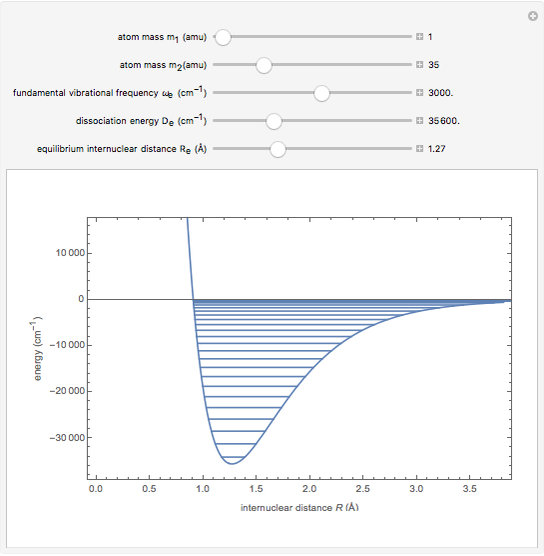
Snapshot 1: vibrational states of 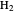
 molecule
molecule
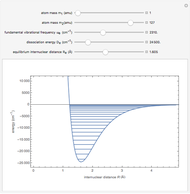
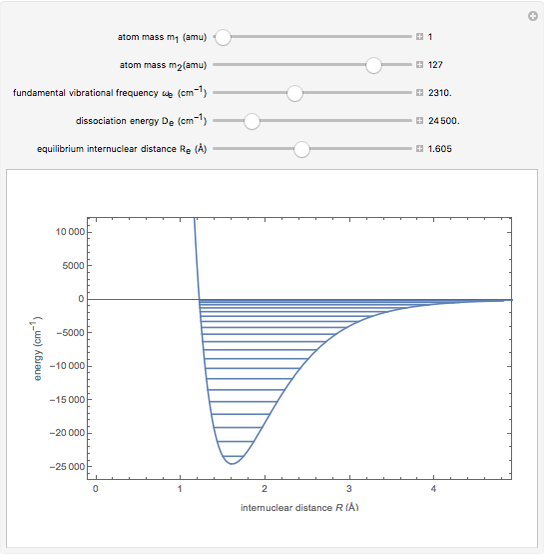
Snapshot 2: HCl molecule
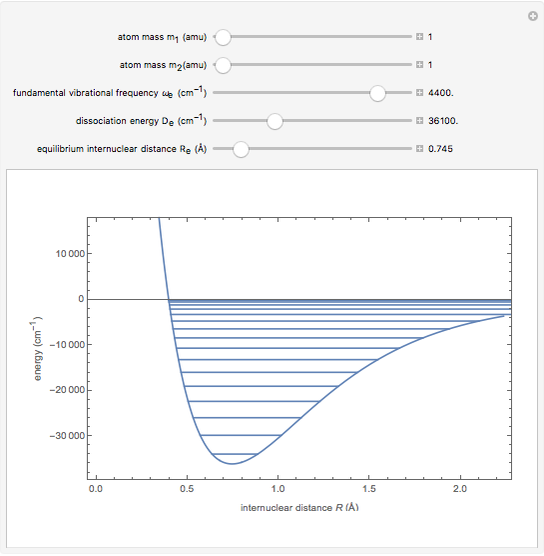
Snapshot 3: HI molecule
Reference: P. M. Morse, "Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels," Phys. Rev., 34(1), 1929 pp. 57–64.
Permanent Citation