Following Chaotic Reflections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
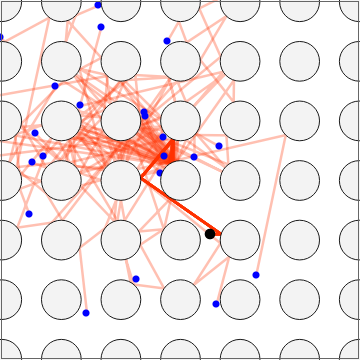
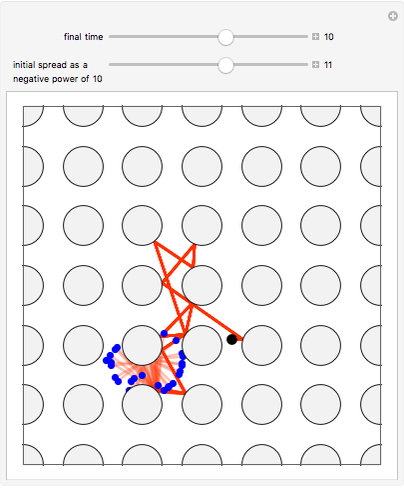
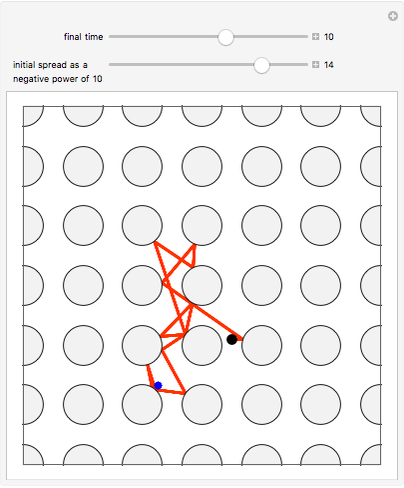
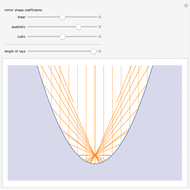
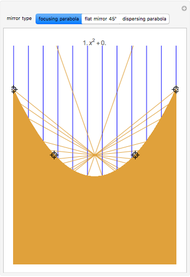
The path traveled by a photon bouncing off a grid of circular mirrors is very sensitive to the initial conditions. The paths shown are of a particle that starts at 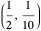 , travels east at speed 1, and reflects off mirrors of radius
, travels east at speed 1, and reflects off mirrors of radius 
 around integer lattice points in the plane. The paths correspond to initial conditions obtained by perturbing each of
around integer lattice points in the plane. The paths correspond to initial conditions obtained by perturbing each of 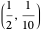 (the starting position) and
(the starting position) and  (the starting direction) to five points around a circle of radius
(the starting direction) to five points around a circle of radius 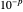 , where
, where 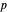 is controlled by the first slider. Thus there are 25 paths shown. When
is controlled by the first slider. Thus there are 25 paths shown. When 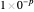 is not so small the paths diverge, which indicates that a
is not so small the paths diverge, which indicates that a 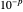 interval is not small enough to guarantee accuracy. When
interval is not small enough to guarantee accuracy. When 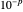 is so small that all 25 paths coincide, it indicates that an interval of that size around the initial conditions is enough to guarantee accuracy in the final result. This illustrates how an interval-based algorithm can lead to correct trajectories. Indeed, the interval algorithm is used to compute all trajectories shown, so they are all correct.
is so small that all 25 paths coincide, it indicates that an interval of that size around the initial conditions is enough to guarantee accuracy in the final result. This illustrates how an interval-based algorithm can lead to correct trajectories. Indeed, the interval algorithm is used to compute all trajectories shown, so they are all correct.
Contributed by: Stan Wagon (Macalester College) (March 2011)
Based on a program by: Folkmar Bornemann and Stan Wagon
Open content licensed under CC BY-NC-SA
Snapshots
Details
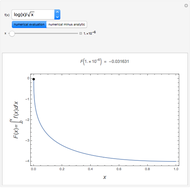
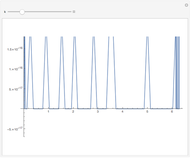
The problem of determining 10 digits of the particle's position at time 10 was one of the SIAM 100-Digit Challenge problems. Using machine precision is inadequate to solve this. Interval arithmetic can be used to provide an algorithm that leads to proved-correct results, even if 10 (the time or the number of digits) is replaced by 1000 or more. The algorithm was developed by F. Bornemann and S. Wagon; see The SIAM 100-Digit Challenge: A Study in High-Accuracy Numerical Computing, by D. Laurie, F. Bornemann, S. Wagon, and J. Waldvogel, SIAM, Philadelphia, 2004.
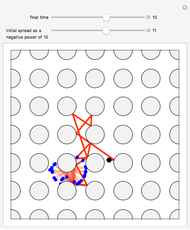
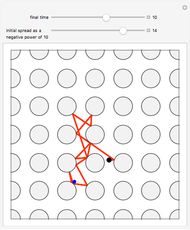
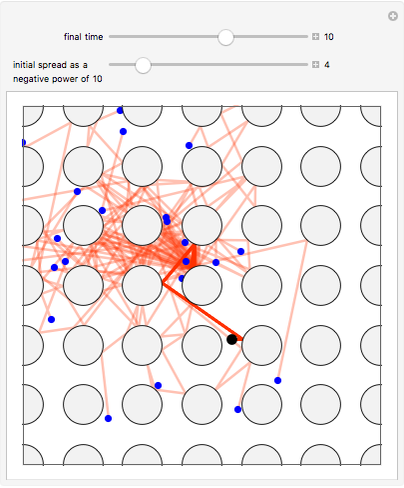
The three snapshots show trajectories out to time 10, with initial spread of 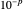 , where p=4, 11, and 14. In the last case the small spread indicates convergence to visual accuracy.
, where p=4, 11, and 14. In the last case the small spread indicates convergence to visual accuracy.
Permanent Citation