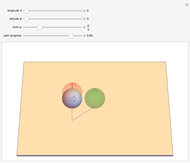
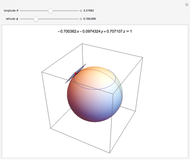
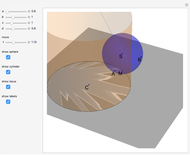
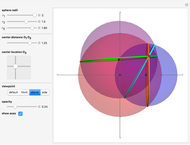
Four Points Determine a Sphere

Initializing live version

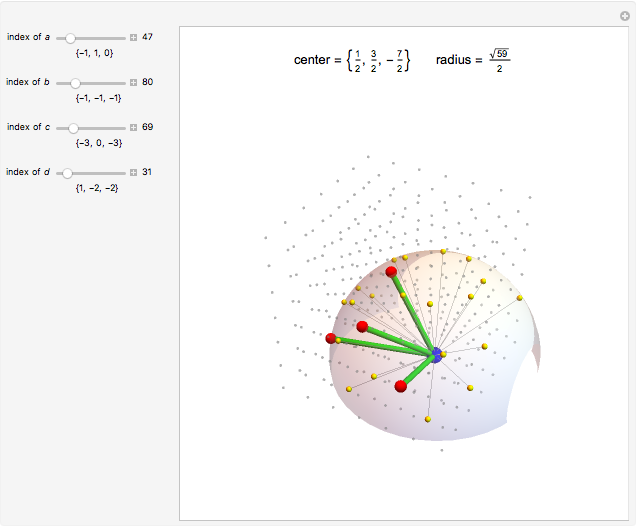
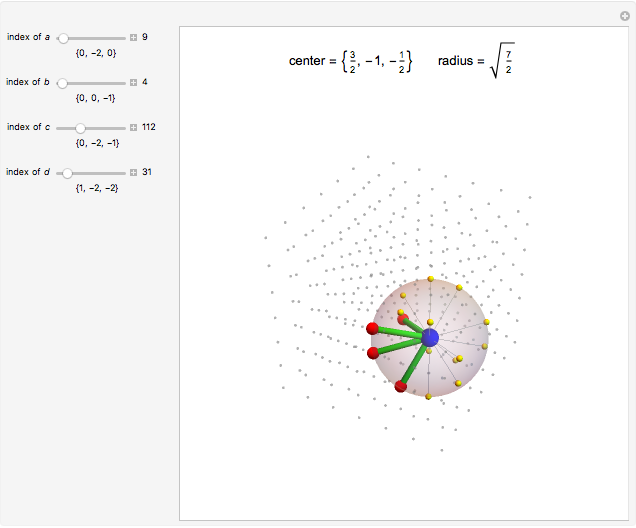
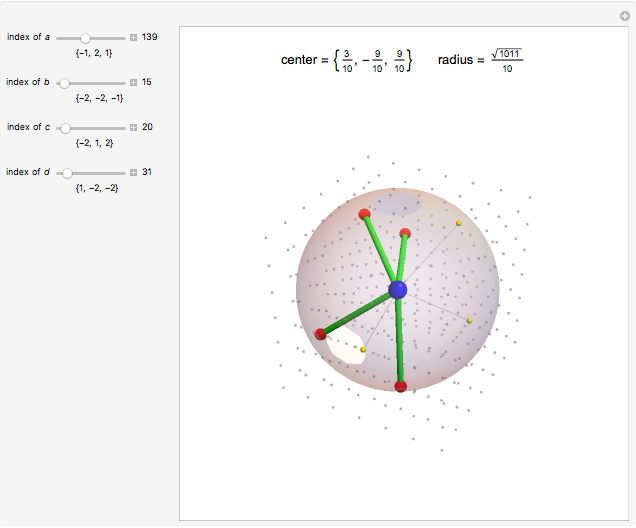
Four noncoplanar points define the surface of a sphere. Each point runs through the 343 possible triples, indexed by 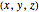where .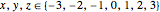

Contributed by: Ed Pegg Jr (October 2016)
Open content licensed under CC BY-NC-SA

Snapshots

detailSectionParagraph


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send