Hermite Interpolation with Pythagorean-Hodograph Cubic Curves
Hermite Interpolation with Pythagorean-Hodograph Cubic Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A polynomial curve 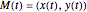 is a Pythagorean-hodograph curve if
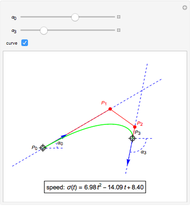
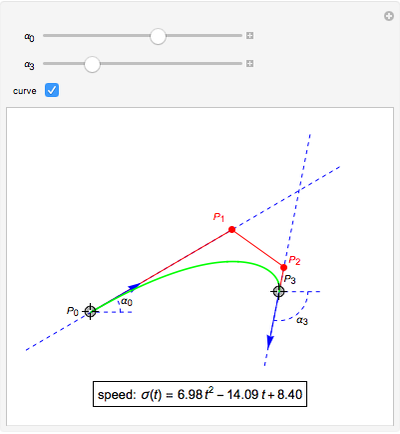
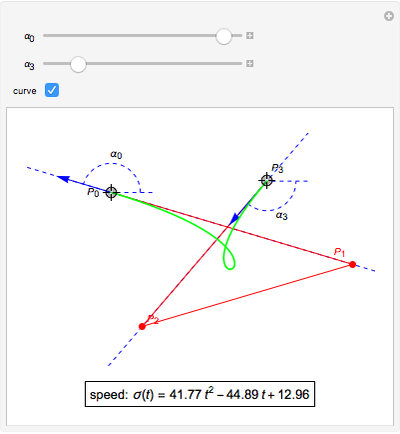
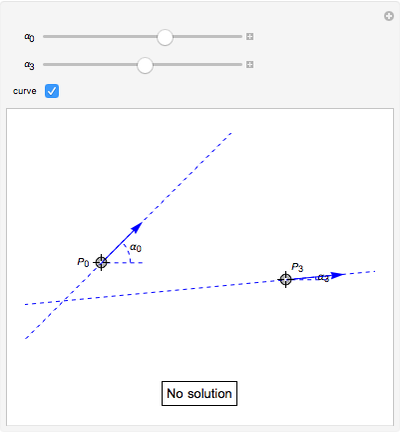
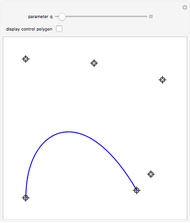
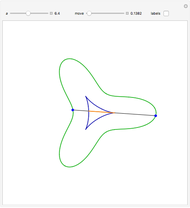
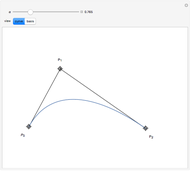
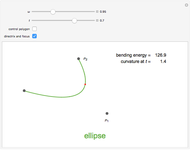
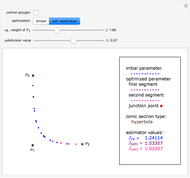
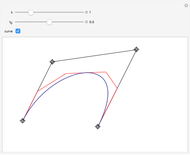
is a Pythagorean-hodograph curve if 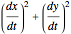 is the square of another polynomial. The lowest-degree curves satisfying this condition are PH-cubics. They are represented here in Bézier form. The degrees of freedom of such a curve allow using it to solve a partial Hermite interpolation problem: the boundary points and the tangent directions can be specified, but not the speeds at these points. Some situations have no solutions.
is the square of another polynomial. The lowest-degree curves satisfying this condition are PH-cubics. They are represented here in Bézier form. The degrees of freedom of such a curve allow using it to solve a partial Hermite interpolation problem: the boundary points and the tangent directions can be specified, but not the speeds at these points. Some situations have no solutions.
Contributed by: Isabelle Cattiaux-Huillard (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a polynomial parametric curve 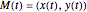 . By definition, its hodograph is its derivative
. By definition, its hodograph is its derivative 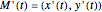 . The curve is called Pythagorean if there exists another polynomial
. The curve is called Pythagorean if there exists another polynomial 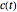 such that
such that 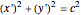 . The curve is then said to have a Pythagorean hodograph or to be a PH curve. Therefore its speed
. The curve is then said to have a Pythagorean hodograph or to be a PH curve. Therefore its speed 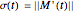 is also a polynomial function of
is also a polynomial function of  . The lowest degree allowing this property is three.
. The lowest degree allowing this property is three.
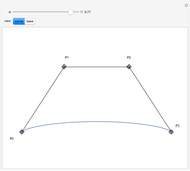
Hence we illustrate here how cubic curves, represented in Bézier form (see Related Link below) by their control polygons 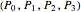 , can be used for a
, can be used for a 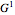 Hermite interpolation. Specifying the boundary points
Hermite interpolation. Specifying the boundary points 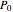 and
and 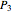 and the two associated unit tangent vector directions, defined by the angles
and the two associated unit tangent vector directions, defined by the angles 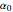 and
and  , we determine the cubic interpolatory PH-curve by its control points
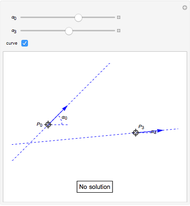
, we determine the cubic interpolatory PH-curve by its control points 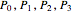 . In certain cases, such a curve cannot exist, because a cubic (PH) curve does not have an inflexion point, so some values of
. In certain cases, such a curve cannot exist, because a cubic (PH) curve does not have an inflexion point, so some values of 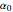 and
and  do not give a solution.
do not give a solution.
References
[1] G. Jaklic, J. Kozak, M. Krajnc, V. Vitrih, and E. Zaga, "On Interpolation by Planar Cubic  Pythagorean-Hodograph Spline Curves," Mathematics of Computation, 79(269), 2010 pp. 305–326.
Pythagorean-Hodograph Spline Curves," Mathematics of Computation, 79(269), 2010 pp. 305–326.
[2] R. T. Farouki, Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable, Berlin: Springer, 2008.
Permanent Citation