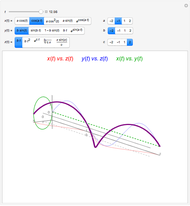
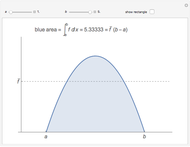
Graphs of Exponential Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
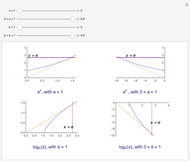
A general exponential function has the form 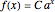 , where
, where 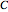 and
and  are positive real numbers. The number
are positive real numbers. The number  is called the exponential base and the number
is called the exponential base and the number 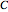 is called the multiplicative constant.
is called the multiplicative constant.
Contributed by: Laura R. Lynch (June 2014)
Open content licensed under CC BY-NC-SA
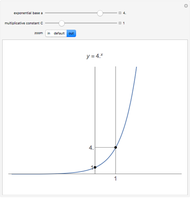
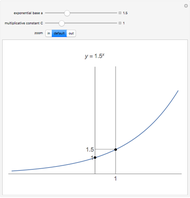
Snapshots
Details
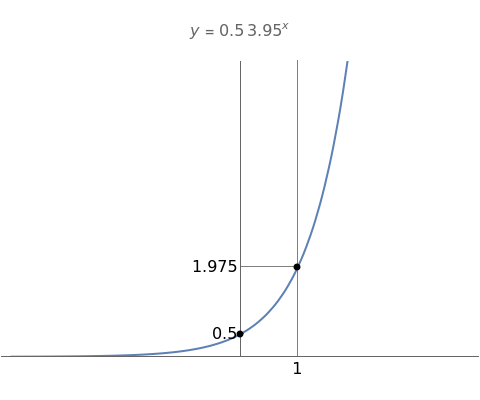
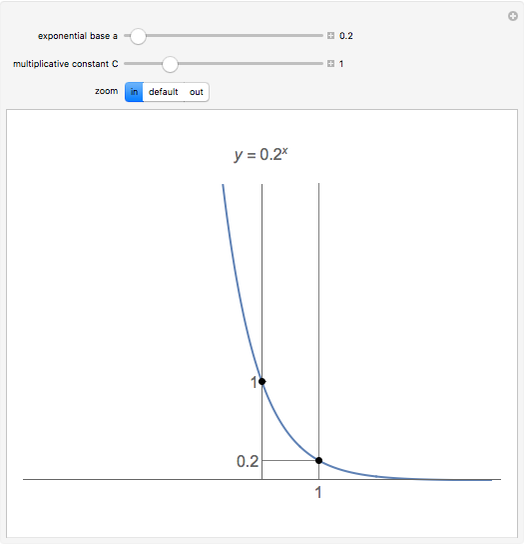
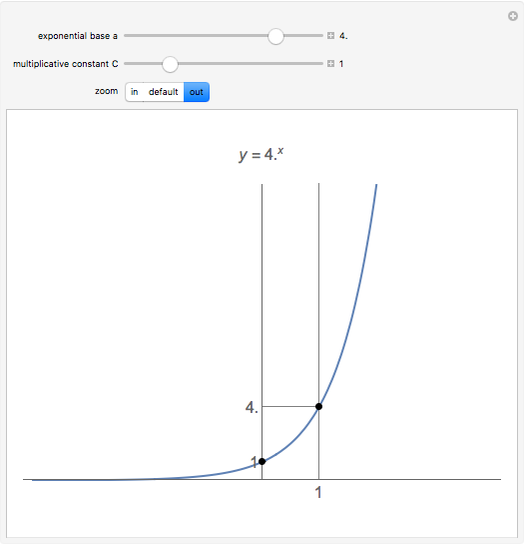
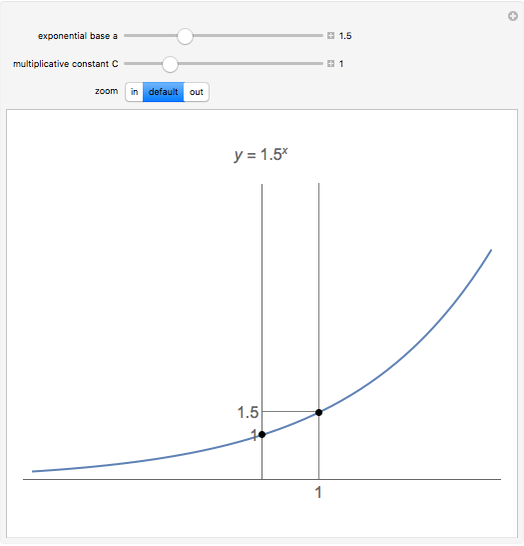
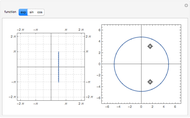
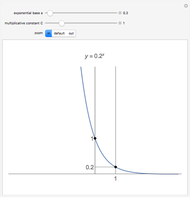
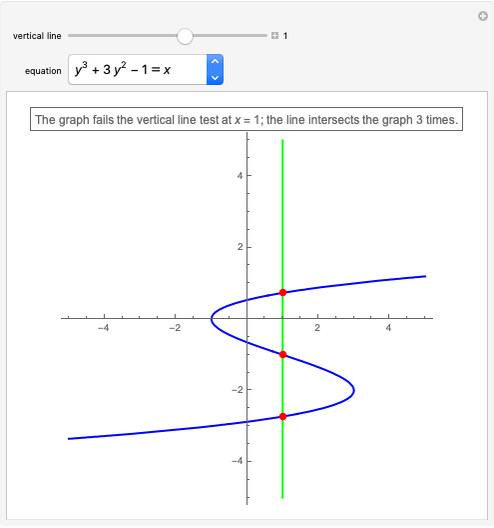
There are two special points to keep in mind to help sketch the graph of an exponential function: At  , the
, the 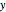 value is
value is 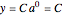 and at
and at 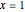 , the
, the 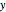 value is
value is 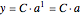 .
.
Here are three other properties of an exponential function:
• The 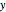 intercept is always at
intercept is always at 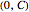 .
.
• There are no  intercepts. In fact, the exponential function has horizontal asymptote at
intercepts. In fact, the exponential function has horizontal asymptote at 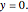
• The graph is always above the  axis.
axis.
Permanent Citation