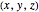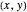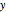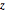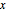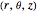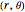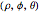Three-Dimensional Coordinate Systems
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
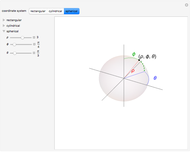
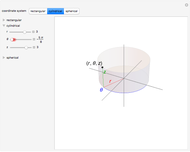
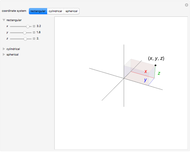
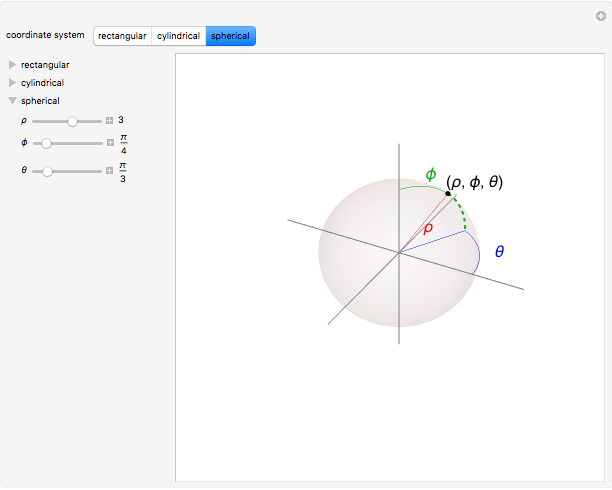
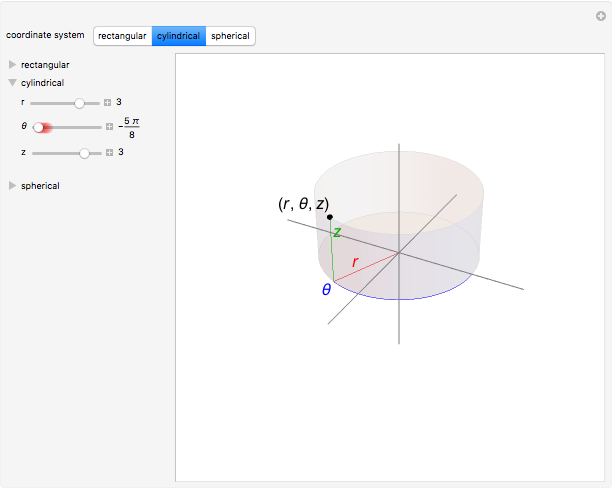
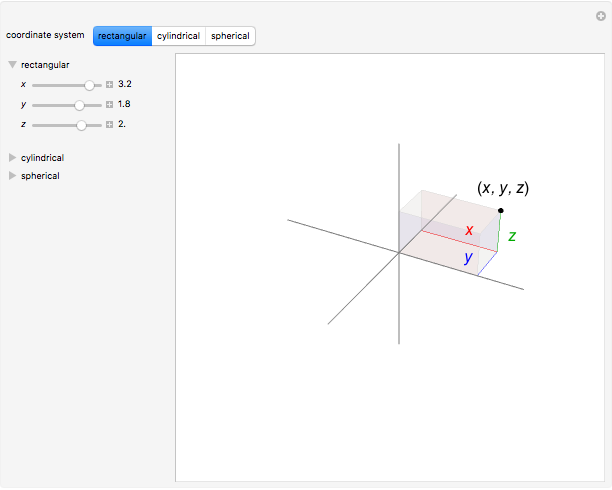
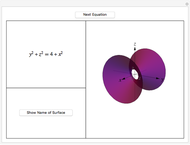
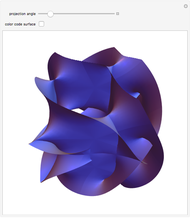
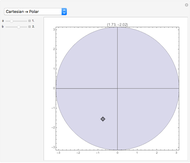
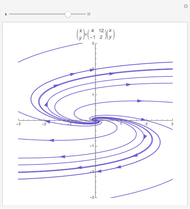
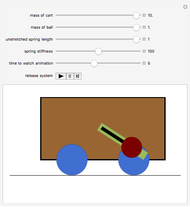
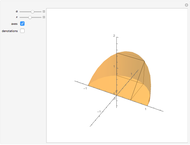
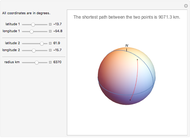
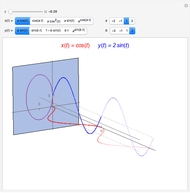
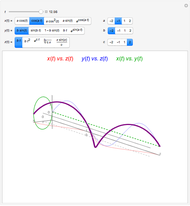
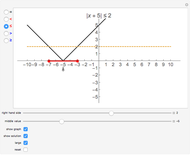
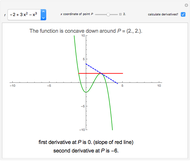
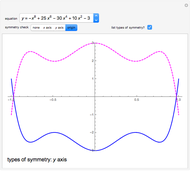
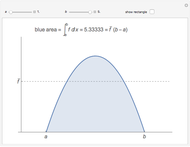
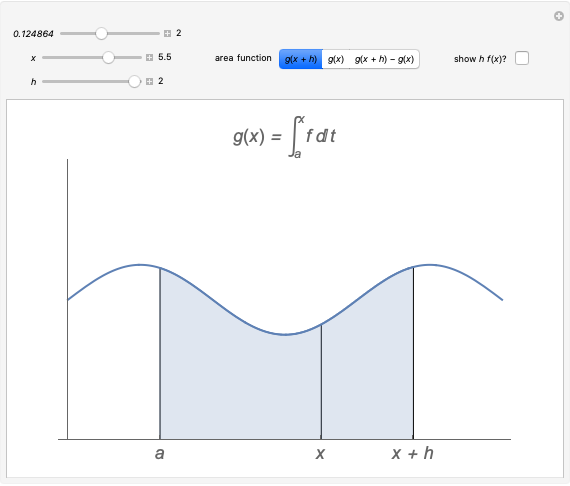
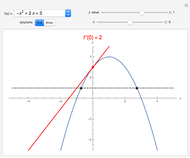
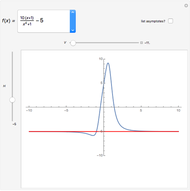
There are three common coordinate systems in three dimensions used in multivariate calculus.
[more]
Contributed by: Laura R. Lynch (May 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation