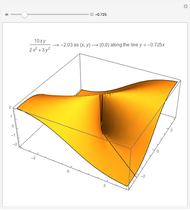
Some Triple Integrals for Mass

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
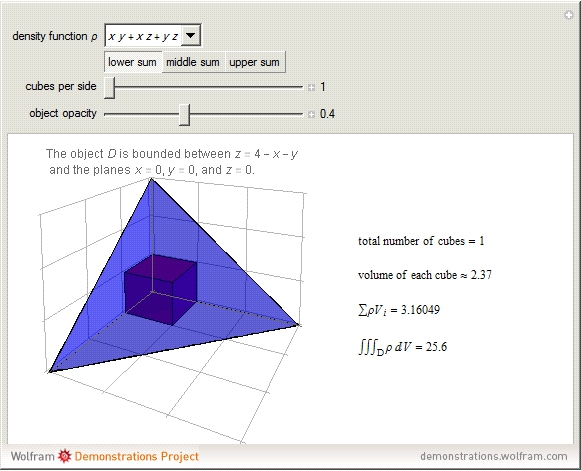
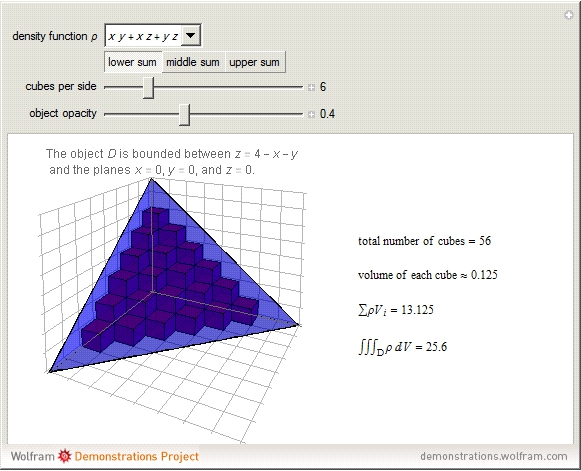
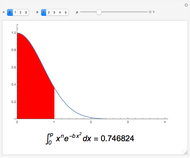
For an object with uniform density, the mass can be calculated as density times volume  . For an object with nonuniform density, calculus is necessary. The idea is to partition the object into enough small cubes so that the density of each cube is approximately uniform. Then, the mass of the object, which is the sum of the masses of each of the cubes, can be approximated by the sum of the density times volume for each individual cube (i.e. if the object is partitioned into cubes
. For an object with nonuniform density, calculus is necessary. The idea is to partition the object into enough small cubes so that the density of each cube is approximately uniform. Then, the mass of the object, which is the sum of the masses of each of the cubes, can be approximated by the sum of the density times volume for each individual cube (i.e. if the object is partitioned into cubes  with density
with density  and volume
and volume  , then the mass of the object is
, then the mass of the object is 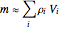 ). The exact mass is the triple integral of the density function.
). The exact mass is the triple integral of the density function.
Contributed by: Laura R. Lynch (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
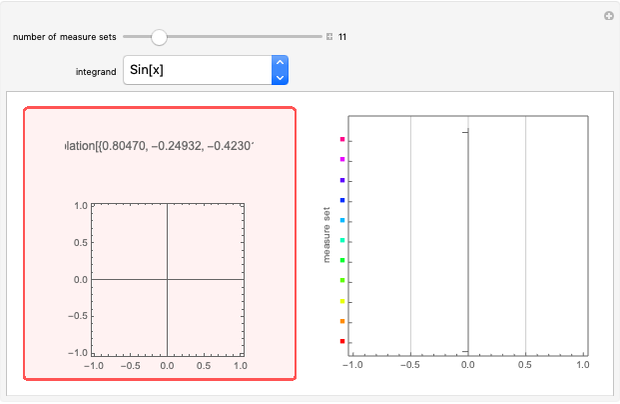
In practice, to find the mass of each individual cube  within a partition, choose a representative point
within a partition, choose a representative point 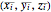 within the cube at which to evaluate the density function. Then,
within the cube at which to evaluate the density function. Then, 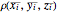 approximates the density of the cube and this approximation improves with smaller and smaller cubes. Thus the mass of an individual cube is
approximates the density of the cube and this approximation improves with smaller and smaller cubes. Thus the mass of an individual cube is 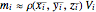 and the mass of the entire object is
and the mass of the entire object is 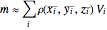 . As the number of cubes increases to infinity, this tends to the triple integral:
. As the number of cubes increases to infinity, this tends to the triple integral:  . This Demonstration chooses the midpoint of each cube as the point
. This Demonstration chooses the midpoint of each cube as the point 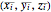 .
.
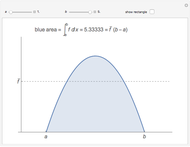
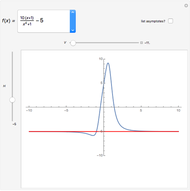
As a special note, snapshot 1 also calculates the volume of the object, because using density function  implies that the mass equals the volume.
implies that the mass equals the volume.
Permanent Citation