A Curious Coin-Flipping Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
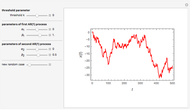
Three players have  ,
, 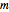 , and
, and  unbiased coins. The players simultaneously flip coins.
unbiased coins. The players simultaneously flip coins.
Contributed by: Heikki Ruskeepää (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
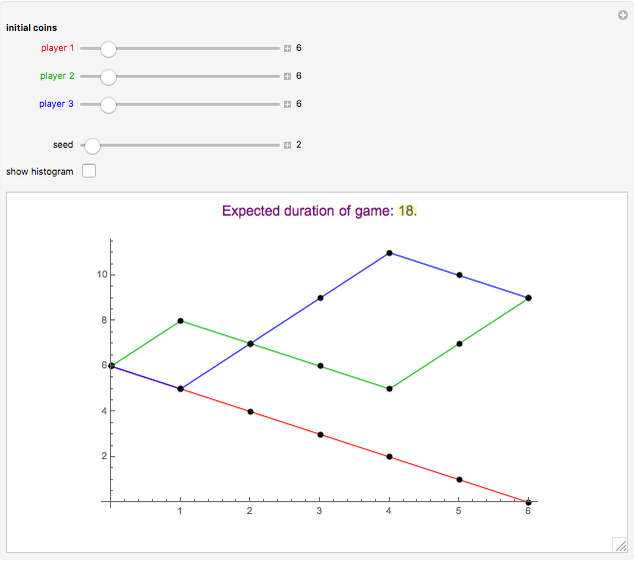
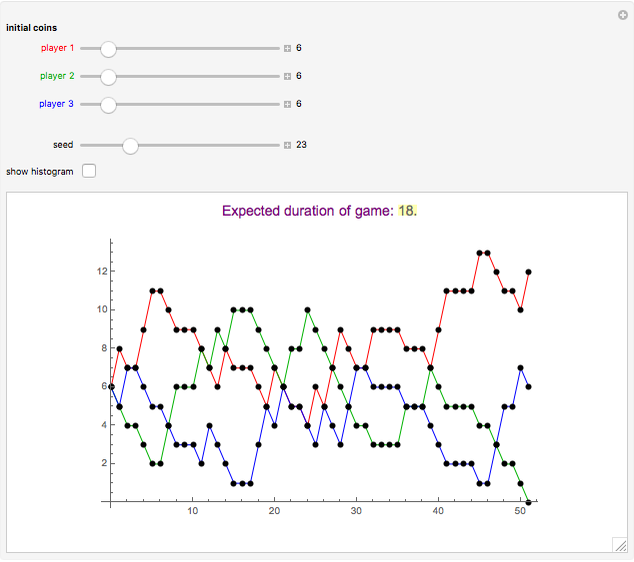
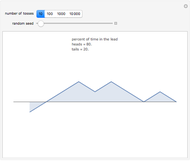
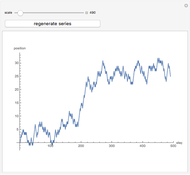
In the first snapshot, the game stopped as soon as possible (in six tosses), but in the second snapshot the game lasted 51 tosses. Note that steps down are one unit while steps up are two units. When the paths remain constant, the outcome was three heads or three tails.
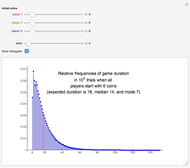
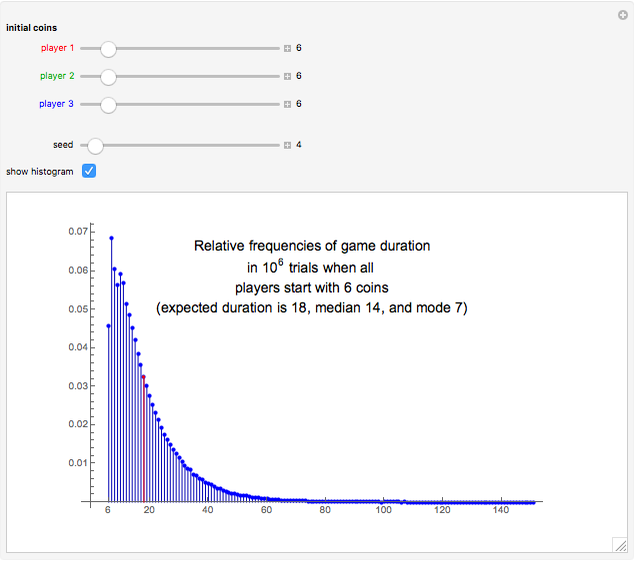
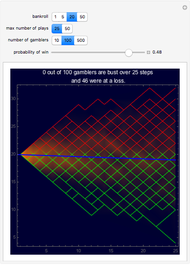
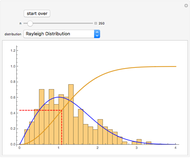
In the third snapshot we see relative frequencies of the duration of the game when each player initially has six coins. These relative frequencies are based on one million simulations of the game (these simulations were done outside of this Demonstration). On average, the game lasted 18 tosses. About half of the games lasted at most 14 tosses and about half at least 15 tosses. The most frequent duration was 7. Interestingly, the histogram is two-peaked, with peaks at 7 and 10 and a local minimum at 9. The shortest duration is 6 but there is no upper bound on the duration; among the one million simulations, one game lasted 151 tosses! However, almost all games last at most, say, 80 tosses (there is a probability of approximately 0.0015 that the game lasts more than 80 tosses).
This Demonstration shows the expected duration of the game, which is  . Its derivation was posed as a problem in the August–September 1941 issue of American Mathematical Monthly (p. 483). This hard problem was solved 25 years later, in 1966 [1]. The solution is cited in problem 4 of [2, pp. 42, 114]; our Demonstration is based on this book.
. Its derivation was posed as a problem in the August–September 1941 issue of American Mathematical Monthly (p. 483). This hard problem was solved 25 years later, in 1966 [1]. The solution is cited in problem 4 of [2, pp. 42, 114]; our Demonstration is based on this book.
References
[1] R. C. Read, "A Type of 'Gambler’s Ruin' Problem," American Mathematical Monthly, 1966 pp. 177–179.
[2] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
Permanent Citation