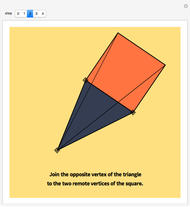
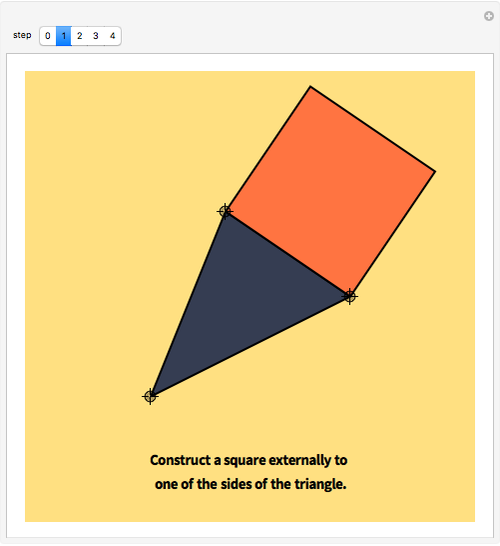
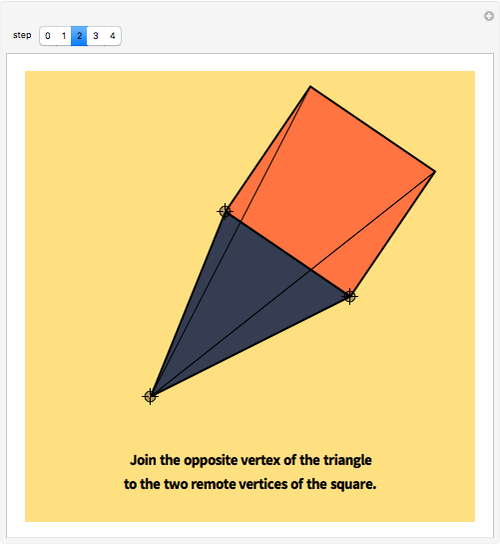
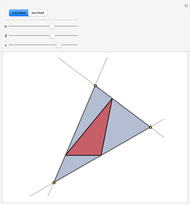
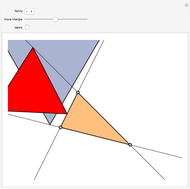
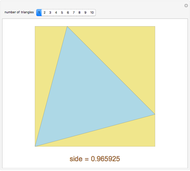
This Demonstration explains the steps involved in obtaining a square inscribed in a triangle using a particular side as its base. The same procedure applies to the other sides and so a triangle can have at most three inscribed squares. It is pointed out when a side of the triangle cannot be the base of an inscribed square.