Poisson Equation on a Circular Membrane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
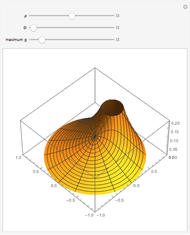
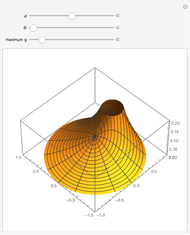
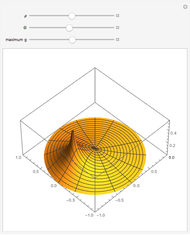
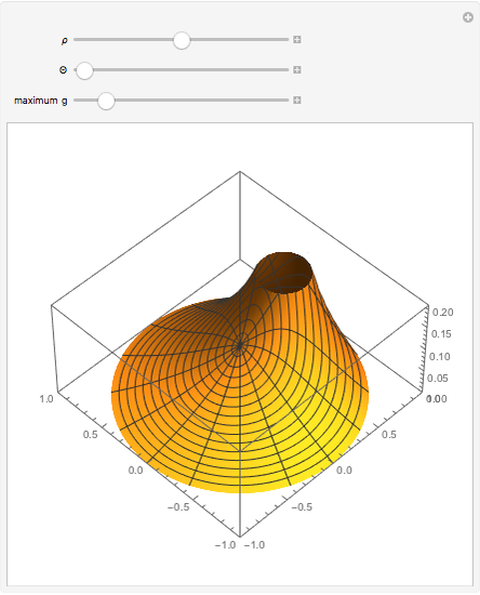
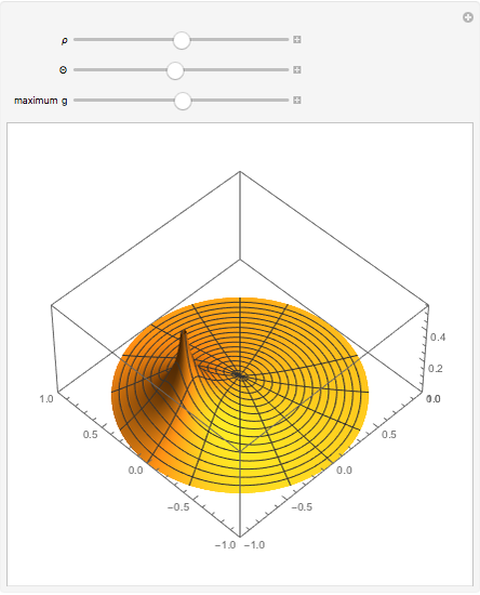
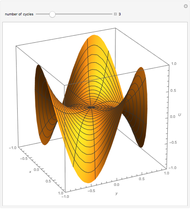
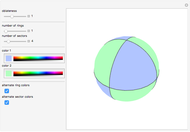
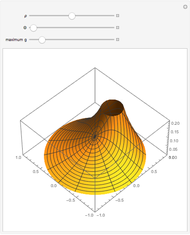
This Demonstration shows the static response (Green's function) of a circular thin membrane to a force applied at a point on the membrane. The boundary is held to zero displacement (Dirichlet boundary condition). The source point is controlled by the  (radius) and
(radius) and  (angle) sliders. The scaling of the response is controlled by the "maximum
(angle) sliders. The scaling of the response is controlled by the "maximum  " slider that controls the response value, which coincides with the top of the viewing box. If the response exceeds this value, it is clipped at the top.
" slider that controls the response value, which coincides with the top of the viewing box. If the response exceeds this value, it is clipped at the top.
Contributed by: David von Seggern (University Nevada-Reno) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The static solution (Green's function) for the Poisson equation for a single force applied on a circular thin membrane at the point ( ,
,  ) is called the Green's function for the circular membrane, which is parameterized by (
) is called the Green's function for the circular membrane, which is parameterized by ( ,
,  ). Poisson's equation for the Green's function
). Poisson's equation for the Green's function  is
is

and the Green's function for the Dirichlet boundary condition, when the circular boundary at radius  is held to zero displacement, is given by (for
is held to zero displacement, is given by (for  )
)
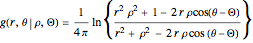 .
.
This solution is, with some manipulation, from Duffy, eq. 5.2.36. Because the solution has no series summation, like many Green's functions for the Poisson equation, it can be computed rather rapidly. The solution depends on  and on the angular difference
and on the angular difference  in such a way that there is little value in enabling the viewer to manipulate
in such a way that there is little value in enabling the viewer to manipulate  , but this is provided anyway. The user can cut
, but this is provided anyway. The user can cut  off at any arbitrary positive value.
off at any arbitrary positive value.
Reference: D. G. Duffy, Green's Functions with Applications, Boca Raton, FL: Chapman & Hall/CRC, 2001.
Permanent Citation