Laceable Knight Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
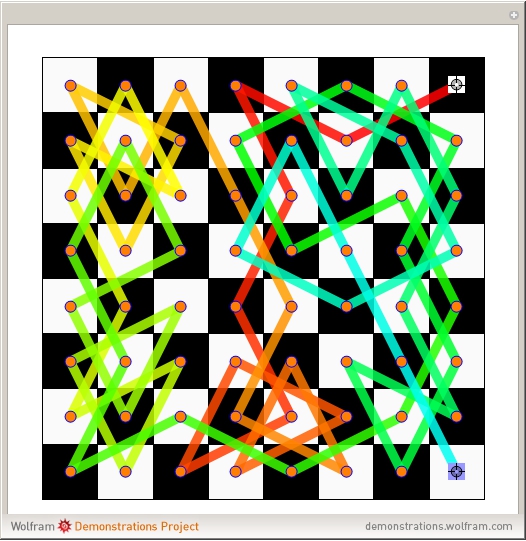
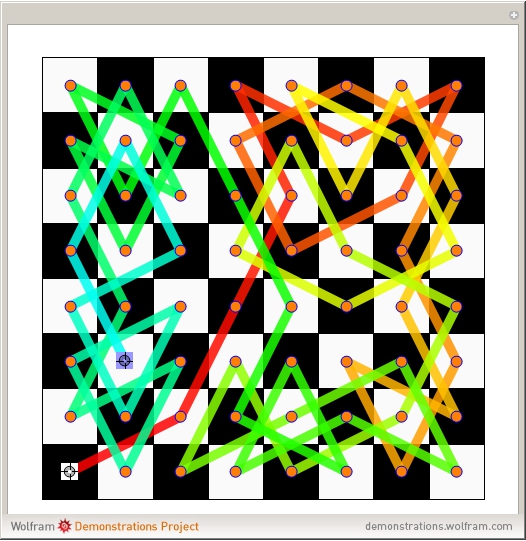
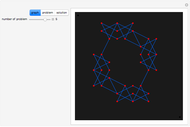
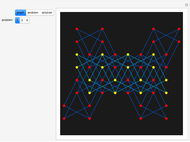
This Demonstration shows how to get from any white square on a chessboard to any black square by a sequence of knight moves that visits all squares. Such a route is called a Hamiltonian path, as opposed to a Hamiltonian cycle, which starts and finishes on the same square. Drag the two locators to change the start and finish squares.
Contributed by: Stan Wagon (July 2012)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let  denote the knight graph: knight moves on an
denote the knight graph: knight moves on an  board, where
board, where 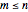 is always assumed. The graph is always bipartite. A bipartite graph having the property that one can get from any point in one part to any point in the other part using a Hamiltonian path is called Hamilton-laceable. This Demonstration shows that
is always assumed. The graph is always bipartite. A bipartite graph having the property that one can get from any point in one part to any point in the other part using a Hamiltonian path is called Hamilton-laceable. This Demonstration shows that  is Hamilton-laceable, thus extending the very old result that
is Hamilton-laceable, thus extending the very old result that  is Hamiltonian.
is Hamiltonian.
By a theorem of A. Schwenk [1], the collection of graphs that admit Hamiltonian cycles consists of 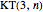 with
with 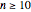 and
and  even;
even;  with
with  odd,
odd, 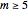 , and
, and  even; and
even; and  with
with  even and
even and  . Of these, I have shown that the following are not laceable:
. Of these, I have shown that the following are not laceable: 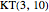 ,
,  ,
,  ,
,  , and
, and  , while the following are laceable:
, while the following are laceable: 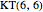 ,
,  ,
,  ,
,  ,
,  , and
, and  . Thus, one conjecture is that the Hamiltonian graph
. Thus, one conjecture is that the Hamiltonian graph  is laceable iff
is laceable iff  .
.
Reference
[1] A. Schwenk, "Which Rectangular Chessboards Have a Knight’s Tour?," Mathematics Magazine, 64(5), 1991 pp. 325–332. www.jstor.org/stable/2690649.
Permanent Citation