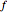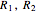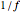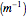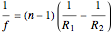Lensmaker's Equation
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
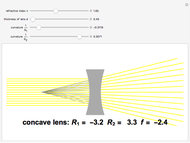
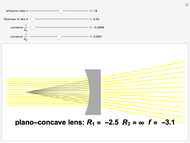
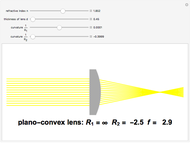
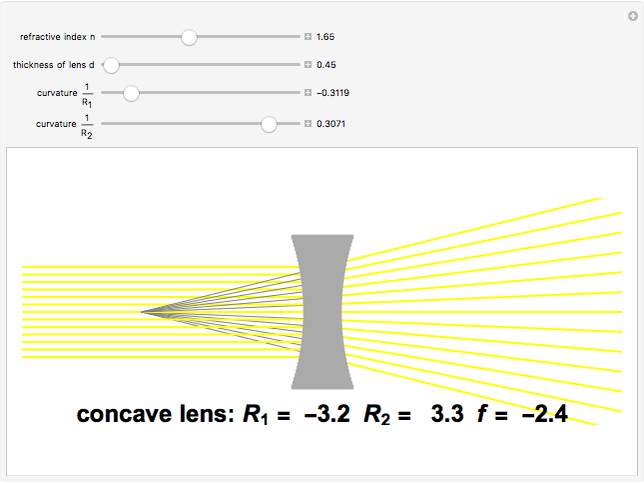
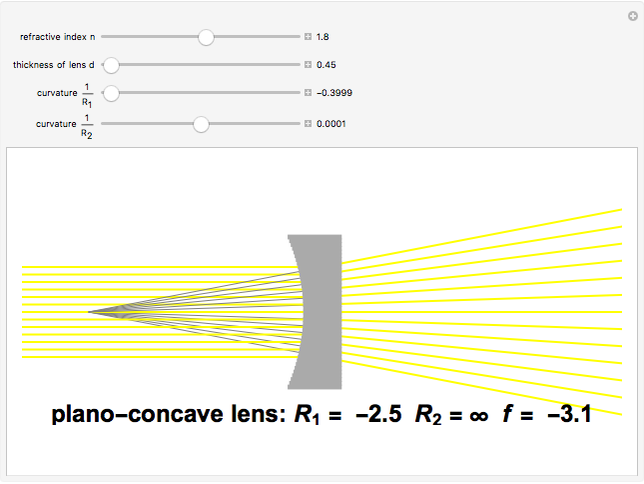
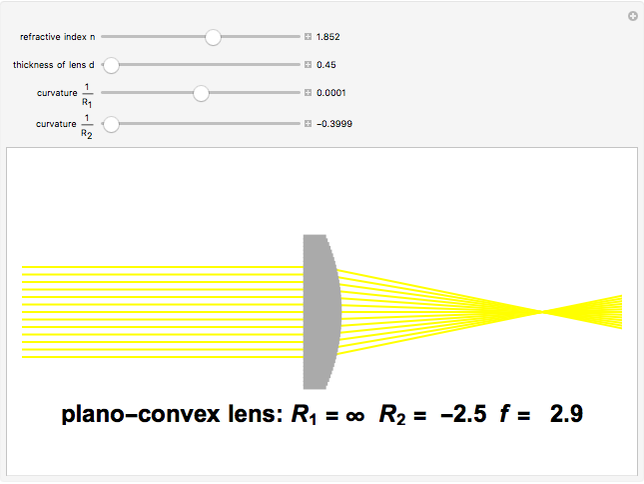
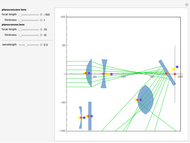
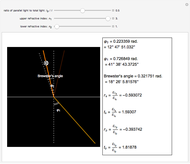
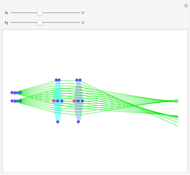
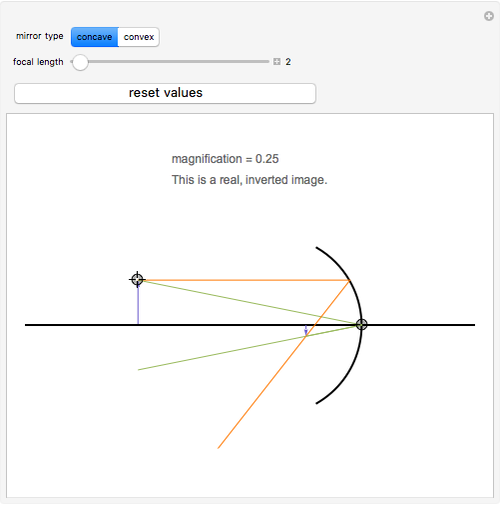
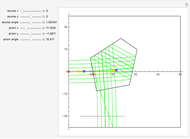
The lensmaker's equation relates the focal length of a simple lens with the spherical curvature of its two faces:
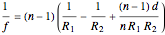 ,
where
,
where 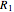 and
and
 represent the radii of curvature of the lens surfaces closest to the light source (on the left) and the object (on the right). The sign of
represent the radii of curvature of the lens surfaces closest to the light source (on the left) and the object (on the right). The sign of  is determined by the location of the center of curvature along the optic axis, with the origin at the center of the lens. Thus for a doubly convex lens,
is determined by the location of the center of curvature along the optic axis, with the origin at the center of the lens. Thus for a doubly convex lens, 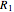 is positive while
is positive while  is negative.
is negative.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation