Pentahex Puzzles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
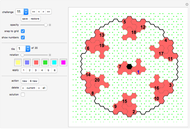
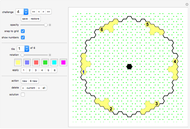
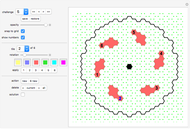
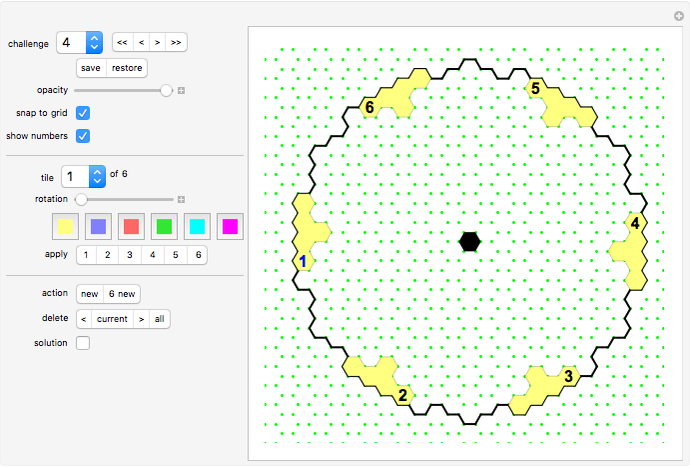
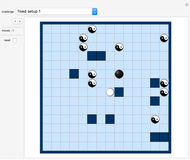
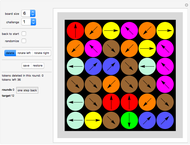
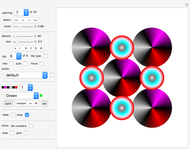
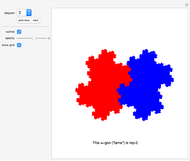
A pentahex is a plane polygon that is the union of five regular hexagons; adjacent hexagons share a common edge. A certain shape can be divided into identical pentahexes in 13 different ways. You are asked to tile the given area (with the central hexagon excluded) with pentahexes. You can drag any tile.
Contributed by: Karl Scherer (June 2013)
After work by: George Sicherman
Open content licensed under CC BY-NC-SA
Snapshots
Details
The given area is the same for all 13 challenges. The solutions were found by George Sicherman. By coloring the tiles with various colors, beautiful patterns emerge (see solutions).
Controls
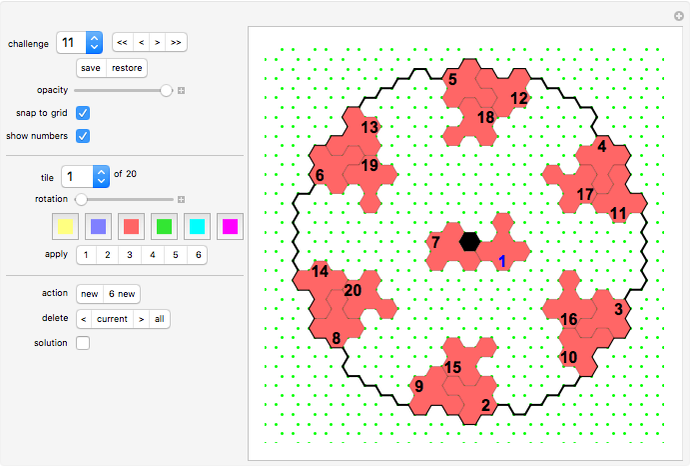
"challenge" drop-down menu There are 13 challenges you can select from the drop-down menu. In each challenge you use copies of a different pentahex tile to fill the given area.
"save/restore" setter bar Option "save" saves the tiling in progress. Option "restore" returns to the most recently saved tiling.
"opacity" slider Here you can select the transparency of the tiles.
"snap to grid" checkbox If this box is checked, the tiles will snap to the given hex grid.
"show numbers" checkbox This checkbox controls whether the tile numbers are visible. Note that the tile numbers indicate the position of the tile handles. All numbers are black except the number of the current tile, which is blue.
"tile" drop-down menu Use this control to select a different tile as the current one.
"rotation" slider This slider rotates and reflects the current tile.
color swatches You can choose from six colors for your tiles.
"apply" Click a number to color the currently edited tile with the associated color.
"action" setter bar Option "new" creates a new tile at the place of the current tile. Option "6 new" creates six copies of the current tile, arranged in a circular manner around the center. Note that the last of these copies will be at the position of the original tile, so that two tiles are then at the same place. Move the surplus one away or delete it (see "delete current").
"delete" setter bar Option "<" deletes all tiles that have a smaller sequence number than the current tile. Option "current" deletes the current tile. Option ">" deletes all tiles that have a greater sequence number than the current tile. Option "all" deletes all tiles.
"solution" checkbox Check this box to show a solution for the selected challenge. Use the "restore" option of the "save/restore" setter bar to return to a saved tiling.
Note This is the first Demonstration based on a hexagonal grid. Drawing the grid and snapping to it is a nontrivial task. How would you program the drawing of the grid and snapping to the grid?
Further Challenges Find out which of the 13 solutions can be extended to a tiling of the whole plane (minus the hexagon at the origin).
History Solutions found by George Sicherman.
Permanent Citation
"Pentahex Puzzles"
http://demonstrations.wolfram.com/PentahexPuzzles/
Wolfram Demonstrations Project
Published: June 14 2013