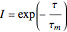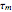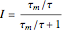Mixing and Segregation in Chemical Reactors (CSTR versus PFR)
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
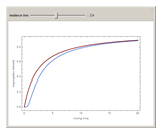
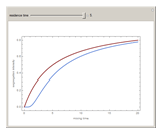
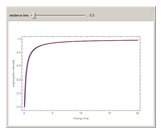
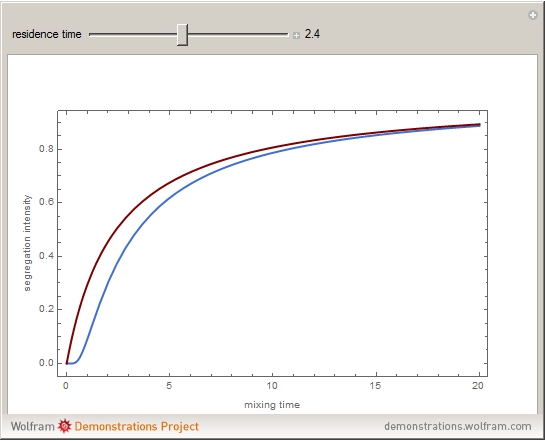
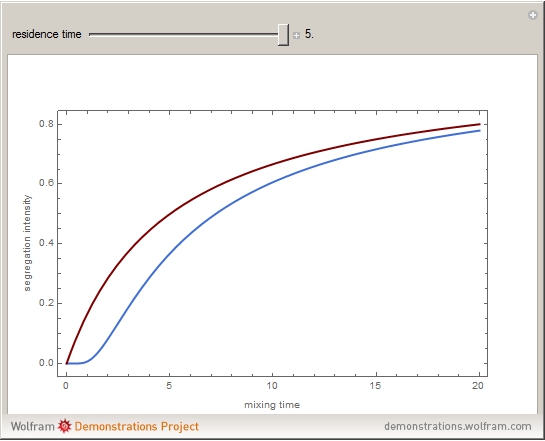
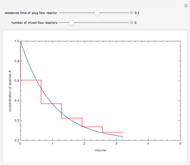
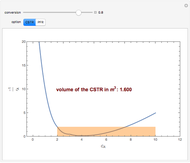
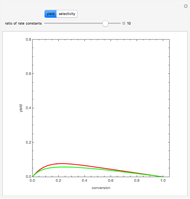
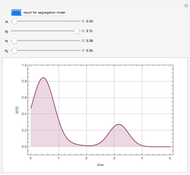
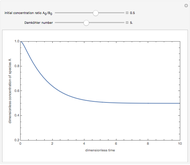
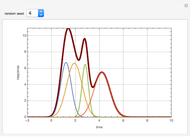
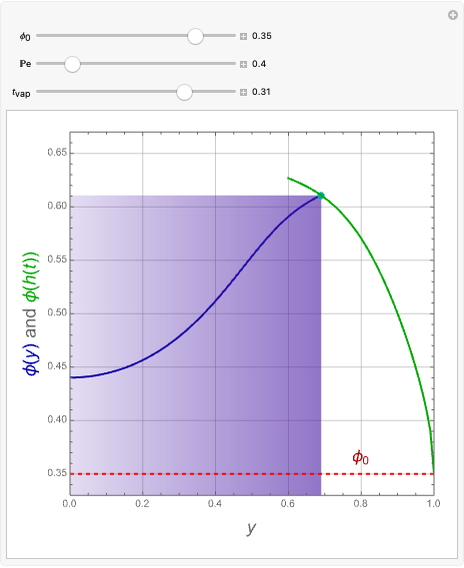
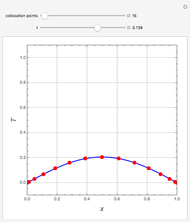
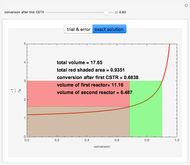
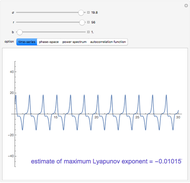
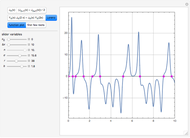
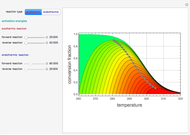
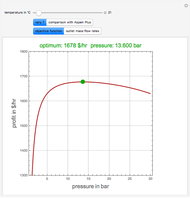
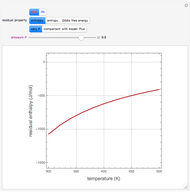
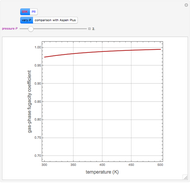
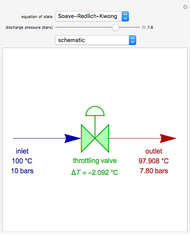
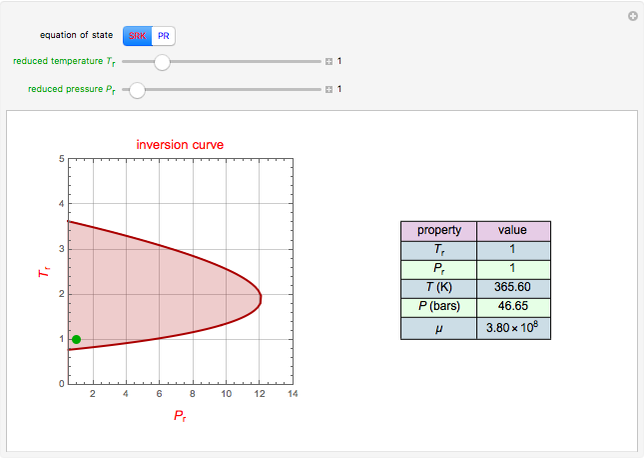
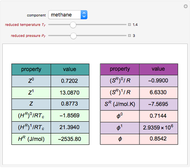
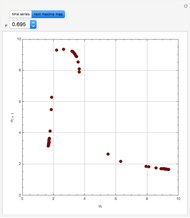
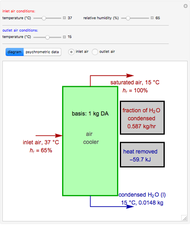
For very fast chemical reactions or viscous liquids, one must take into account the segregation of reactants. The intensity of segregation varies between 0 (perfect mixing) and 1 (no mixing). Mixing intensity can influence reaction rates and selectivities.
[more]
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
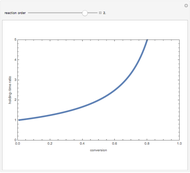
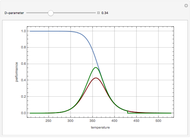
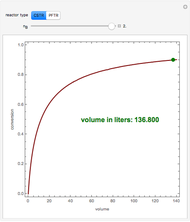
Snapshots
Details
J. Ingham, I. J. Dunn, E. Heinzle, and J. E. Prenosil, Chemical Engineering Dynamics, 2nd ed., Weinheim, Germany: Wiley-VCH, 2000 pp. 444–449.
Permanent Citation