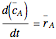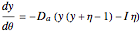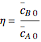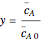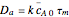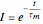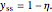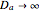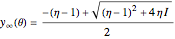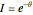Simple Reaction with Segregation in a Batch Reactor
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
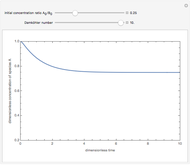
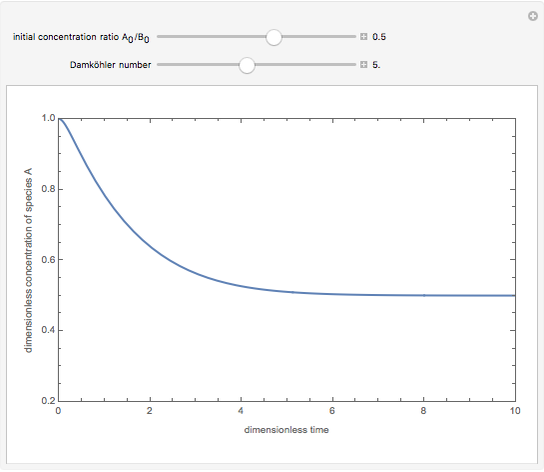
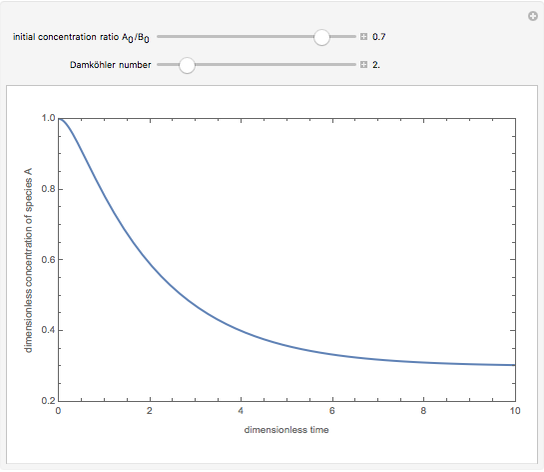
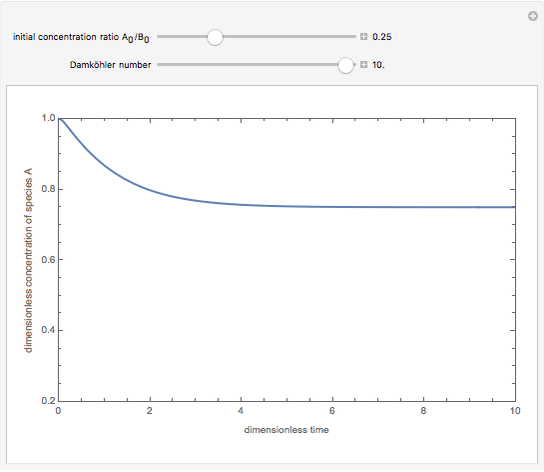
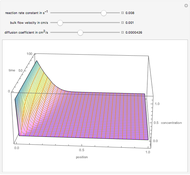
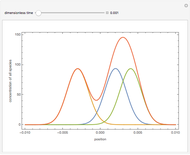
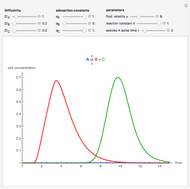
Consider a simple chemical reaction  in a batch reactor. The reaction rate in terms of the intensity of mixing,
in a batch reactor. The reaction rate in terms of the intensity of mixing, 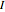 , is given by:
, is given by: 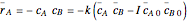 , where
, where 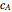 and
and 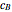 are the instantaneous concentrations,
are the instantaneous concentrations, 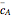 and
and 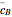 are the mean concentrations, and
are the mean concentrations, and  and
and 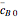 are the initial concentrations of species
are the initial concentrations of species 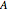 and
and 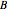 . The governing equation is the following:
. The governing equation is the following:
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
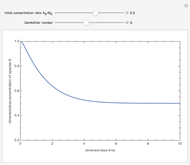
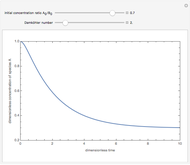
Snapshots
Details
J. Ingham, I. J. Dunn, E. Heinzle, and J. E. Prenosil, Chemical Engineering Dynamics, 2nd ed., Weinheim, Germany: Wiley-VCH, 2000 pp. 450–451.
Permanent Citation