Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Multiset Partitions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

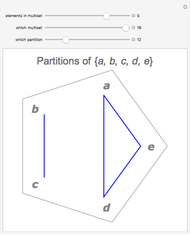
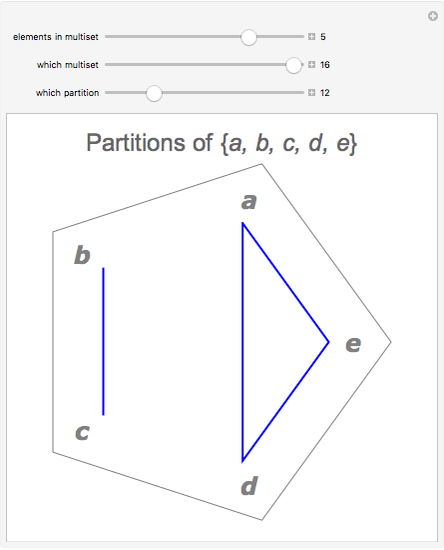
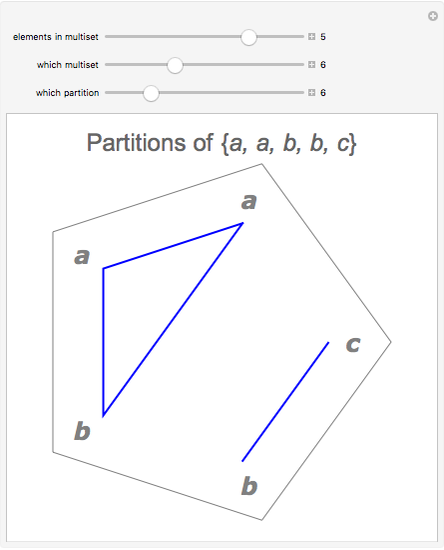
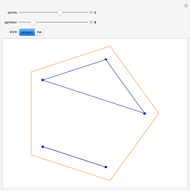
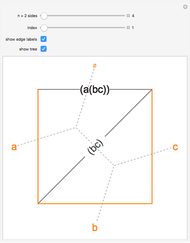
A multiset is an orderless collection of elements in which elements may be repeated, as in 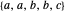. In this Demonstration, the elements of the multiset are arranged at the corners of a regular 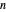-gon. Elements in the same submultiset are connected with line segments (singletons appear as dots).

Contributed by: George Beck and Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

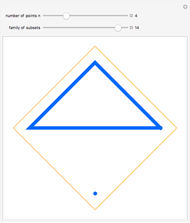
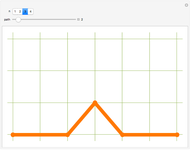
Snapshot 1: when a multiset containing 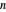elements is a set—that is, no elements are repeated—the number of partitions is the 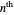Bell number, calculated with the Mathematica function BellB

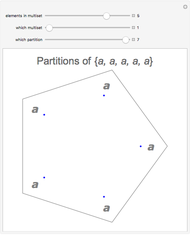
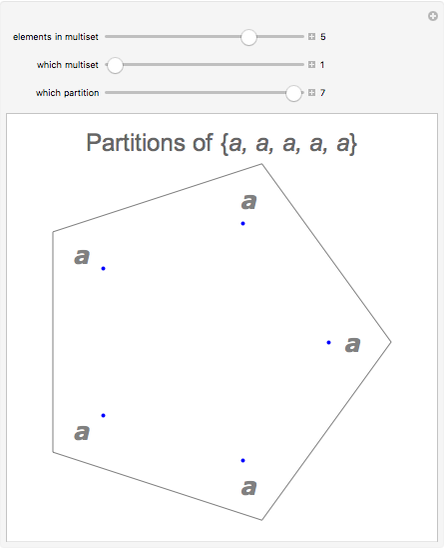
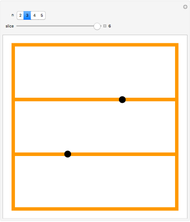
Snapshot 2: at the other extreme is a multiset consisting of the same element repeated 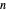times, which has 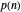distinct partitions, where 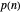is the number of partitions of the integer 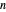, calculated with the Mathematica function PartitionsP

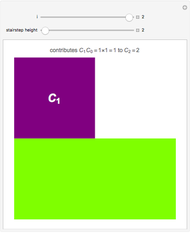
Snapshot 3: the general case has more than two elements with some element occurring more than once

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send