Insurance Disclosures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
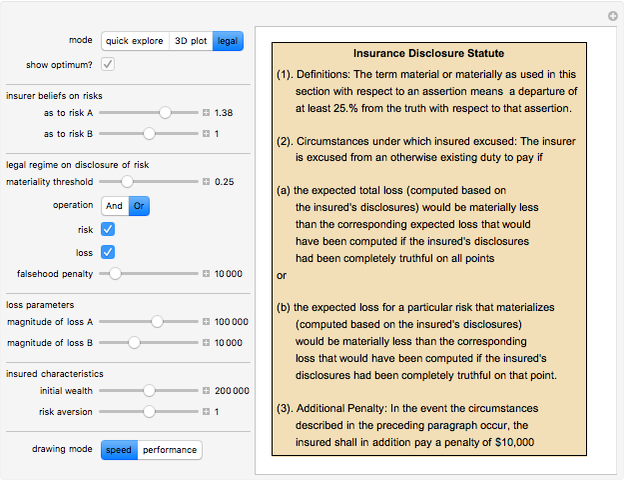
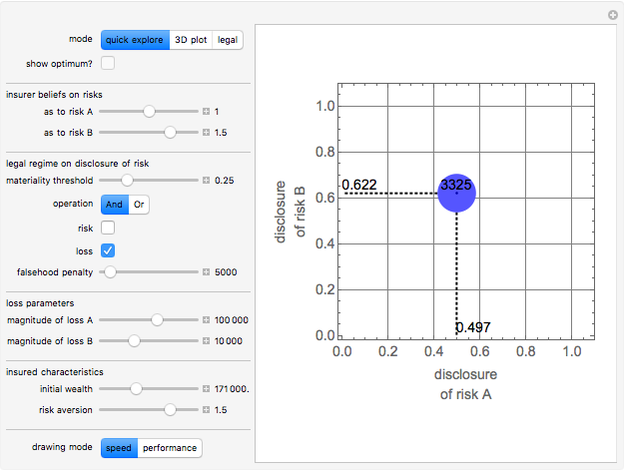
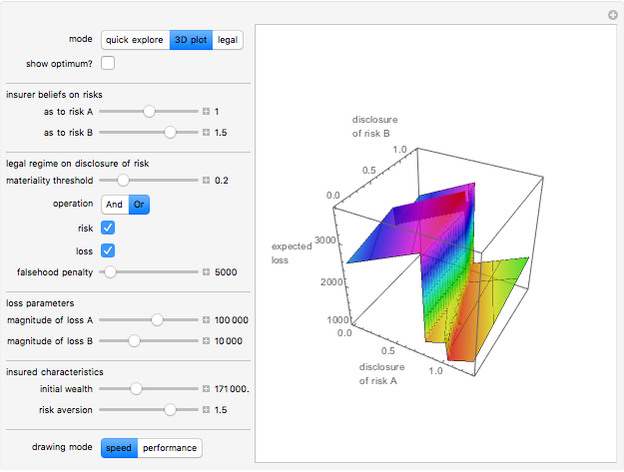
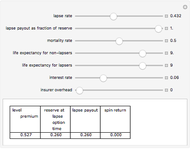
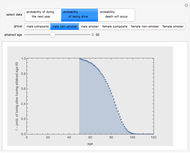
Prospective insureds often have a choice about how truthful to be in their application for insurance. Morality aside, is it ever optimal for applicants to understate the risks they pose? This Demonstration examines this issue by idealizing a world in which the insured chooses how truthful to be with respect to two possible insured events, A and B, the probabilities of which are statistically independent and at most one of which can materialize. By moving the sliders labeled "insurer belief on risks", you determine whether this mapping is accurate (sliders set to 1), underestimates the true expected loss (sliders set below 1), or overestimates the true expected loss (sliders set above 1). You can also choose a set of parameters relating to the law of disclosure. These include how material an underdisclosure has to be before the insurer is excused from an otherwise existing duty to pay a claim, whether a material underdisclosure as to the total expected loss faced by the insurer creates "excuse", and whether a material underdisclosure as a particular loss that materializes creates "excuse".
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
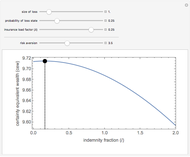
Snapshots
Details
Crude categorization can lead an insurer to overstate the expected loss caused by various disclosures. The insurer might have an underwriting plan, for example, under which ownership of various dog breeds is thought to create high expected losses. The insured might know, however, that their pit bull mix had been remarkably well-trained and was thus extremely unlikely to bite. The model explores the circumstances under which it might be wealth-maximizing for the insured to misstate the dog's breed.
In a typical homeowner insurance policy, the A event might be the homeowner incurring liability to another and the B event might be the home sustaining physical injury from a peril covered by the policy. In a life insurance policy, the A event might be death from disease such as cancer or heart disease and the B event might be death from traumatic injury. The insurer maps the disclosures made by the insured with respect to each event into a belief as to the expected loss caused both by that event and by all events. By way of example, if the insured disclosed that they owned a pit bull, the homeowner's insurer might assess liability risk to be high whereas if they neglected to make such a disclosure or said that they had a Basset Hound, the homeowner's insurer might assess liability risk to be low. Alternatively, if the insured disclosed the insured's parents both died young of heart disease the life insurer might assess disease risk to be high whereas if the insured neglected to make that disclosure the life insurer might assess disease risk to be low.
In most American jurisdictions, an inaccurate disclosure excuses the insurer from an otherwise existing duty to pay if a truthful disclosure would have resulted in a significantly different underwriting decision, such as a non-trivially higher premium, additional restrictions being added to the policy, or a refusal to insure at all. The insurer can "seize" upon such a misrepresentation even if it has nothing to do with the claim that materializes. Such use of the misrepresentation is sometimes referred to (generally in a derogatory sense) as "post-claim underwriting". These jurisdictions can be represented in the Demonstration by making sure that the "risk" box is checked in the legal regime segment of the controls. In some jurisdictions, however, the misrepresentation must relate to the loss that ultimately occurred and thus even a material misrepresentation as to a loss that did not materialize would not excuse the insurer from an otherwise existing duty to pay a claim. These jurisdictions can be represented in the Demonstration by making sure that the "risk" box is unchecked and the "loss" box is checked. The Demonstration lets you play with various alternative interactions between failure accurately to state overall risk and failure accurately to state risk relating to a loss that materializes.
Although it is not particularly common, the result of a material misstatement on an insurance application can not only be the creation of a lawful excuse on the part of the insurer not to pay a claim, it can also result in criminal punishment of the insured. You can simulate criminal punishment by manipulating the "falsehood penalty" control. The control measures the expected monetary equivalent of any punishment associated with detected insurance fraud beyond the extinguishment of an otherwise legitimate claim.
The utility function used in this Demonstration exhibits what is known as constant relative risk aversion (CRRA). You can increase the risk aversion of the insured by increasing the risk aversion coefficient in the controls.
Minimization of the insured's expected diminution in certainty equivalent wealth resulting from disclosures is computed using the Nelder–Mead method of global optimization.
Snapshot 1: the Demonstration in "legal" mode, showing the text of a statute roughly corresponding with the chosen parameters
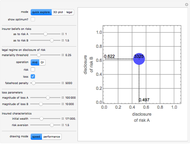
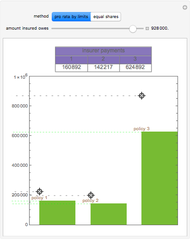
Snapshot 2: the Demonstration in "quick explore" mode showing the expected cost (premium plus expected losses) associated with various parameters and user-specified levels of disclosure as to risk A and risk B
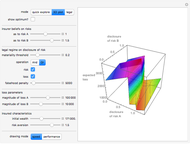
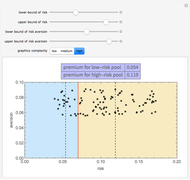
Snapshot 3: the Demonstration in "3D plot" mode
Permanent Citation
"Insurance Disclosures"
http://demonstrations.wolfram.com/InsuranceDisclosures/
Wolfram Demonstrations Project
Published: March 7 2011