Optical Activity of Tartaric Acid Stereoisomers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
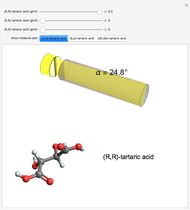
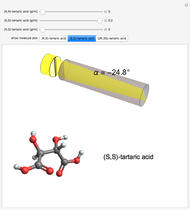
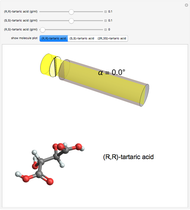
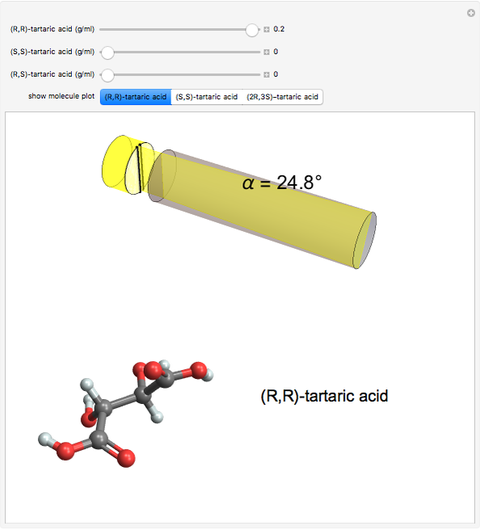
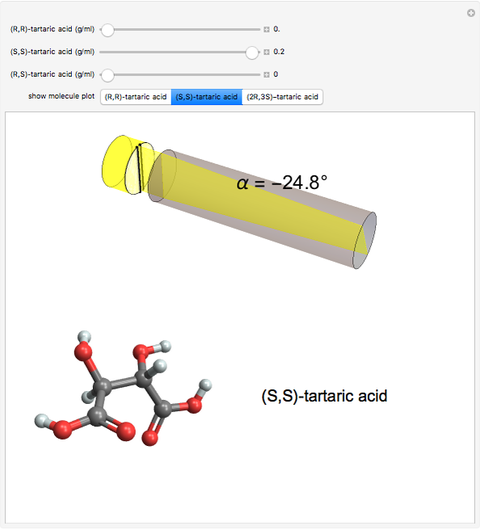
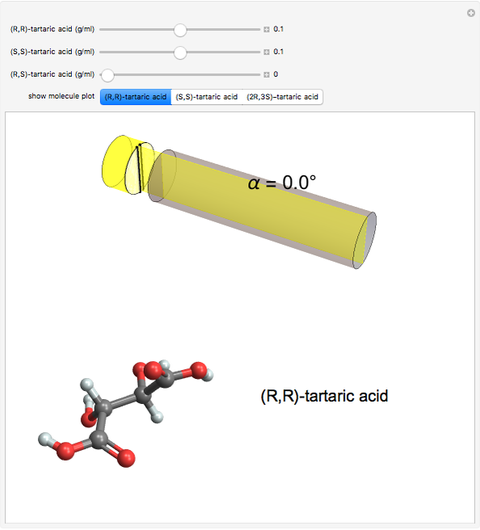
Optical activity of compounds in solution can be measured with a polarimeter, shown schematically in the upper part of the graphic. The angle of rotation of plane polarized light, conventionally the sodium D-line at 589 nm, is determined using two polarizers. (In the graphic, an idealized incident polarizer is reduced to a vertical slit coincident with the plane of polarization.) The angle of polarization of the emerging light is given by 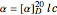 , where
, where  is the specific rotation, referred to the sodium D-line and a temperature of 20 ºC,
is the specific rotation, referred to the sodium D-line and a temperature of 20 ºC, 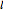 is the path length in decimeters (set equal to 10), and
is the path length in decimeters (set equal to 10), and  is the concentration in g/ml. The tartaric acid molecule has three possible stereoisomers:
is the concentration in g/ml. The tartaric acid molecule has three possible stereoisomers:
Contributed by: S. M. Blinder (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Louis Pasteur in 1848, using a pair of tweezers and a magnifying glass, was able to separate individual crystals of sodium ammonium tartarate tetrahydrate that were mirror images of one another. (Tartaric acid is found in wine, one of the earliest targets of pasteurization.) Pasteur found that, in water solution, the two varieties were optically active, with equal concentrations of the two different forms rotating the plane of linearly polarized light by exactly the same angle, but in opposite directions. Later, van 't Hoff and Le Bel proposed that the different forms—called stereoisomers—of optically active compounds were right- and left-handed versions of the same molecules, with the chirality (handedness) originating from asymmetric carbon atoms bonded to four nonidentical groups.
Tartaric acid HOOC-C*H(OH)-C*H(OH)-COOH (2,3-dihydroxybutanedioic acid) has two asymmetric carbon centers, which are marked with asterisks. Since 1966, the nomenclature for absolute configuration of stereoisomers have been based on the Cahn–Ingold–Prelog system. This replaces the older D (dextro) and L (levo) classification (which is still in use in some biochemical literature). According to the modern system, the four groups attached to the asymmetric carbon are classified by priority, numbered 1 through 4. The details of this classification are given in any up-to-date organic chemistry textbook. For present purposes, we need only consider the four groups around the asterisk-marked carbon atoms in tartaric acid, which have the priority ordering OH > COOH > CH(OH)COOH > H. Now imagine the lowest 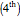 priority substituent (H) to be the steering column of an automobile and the
priority substituent (H) to be the steering column of an automobile and the 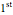 ,
,  , and
, and 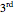 priority groups to be arrayed around the steering wheel. If the ordering 1
priority groups to be arrayed around the steering wheel. If the ordering 1  2
2  3 is clockwise, as if performing a right turn, the configuration is called R (Latin rectus = right). If it is counterclockwise, as in a left turn, the configuration is called S (Latin sinister = left).
3 is clockwise, as if performing a right turn, the configuration is called R (Latin rectus = right). If it is counterclockwise, as in a left turn, the configuration is called S (Latin sinister = left).
Snapshot 1: (S,S)-tartaric acid, showing a negative optical rotation
Snapshot 2: a racemic mixture of (R,R) and (S,S), showing zero net rotation
Snapshot 3: meso-tartaric acid, the (R,S) form, which is optically inactive
See any modern textbook on organic chemistry.
Permanent Citation