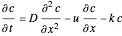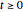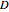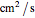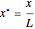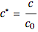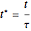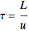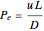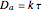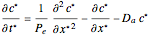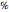Packed Bed Reactor with Longitudinal Mixing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
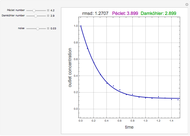
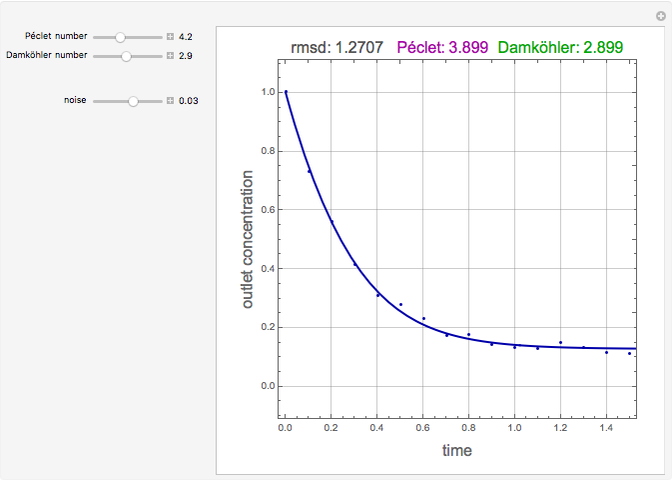
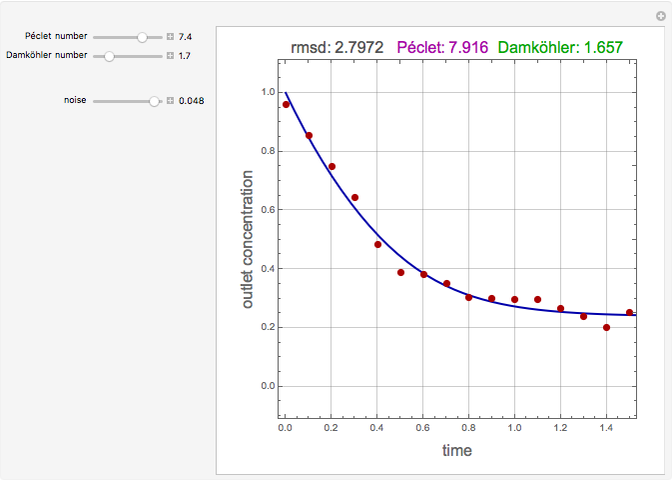
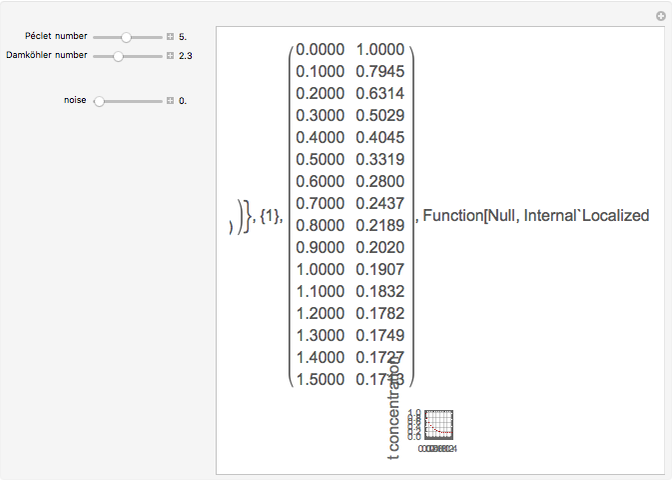
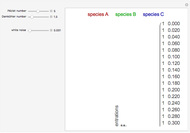
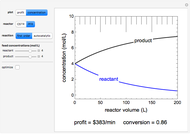
Consider an isothermal packed bed reactor (PBR) in which an irreversible first-order reaction 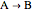 is taking place. The reaction rate is given by
is taking place. The reaction rate is given by 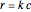 , where
, where  is the rate constant and
is the rate constant and  is the concentration of species
is the concentration of species  . The reactor's length is
. The reactor's length is 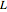 . Assume that pure reactant
. Assume that pure reactant  enters at
enters at 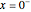 with a concentration
with a concentration 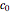 . For a closed-closed vessel, the Danckwerts boundary conditions at the two ends of the reactor are
. For a closed-closed vessel, the Danckwerts boundary conditions at the two ends of the reactor are 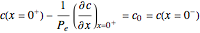 and
and 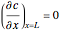 . The turbulent flow of the fluid in the pipe is characterized by the velocity
. The turbulent flow of the fluid in the pipe is characterized by the velocity  . The concentration profile
. The concentration profile 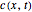 in this PBR is governed by the following partial differential equation:
in this PBR is governed by the following partial differential equation:
Contributed by: Housam Binous, Farrukh Shehzad, Mohammad Mozahar Hossain, Abdullah A. Shaikh, and Ahmed Bellagi (January 2016)
(King Fahd University of Petroleum & Minerals, KSA; ENIM, University of Monastir, Tunisia)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation