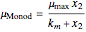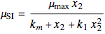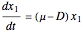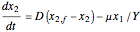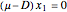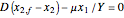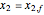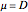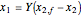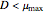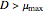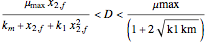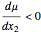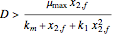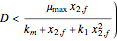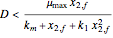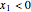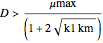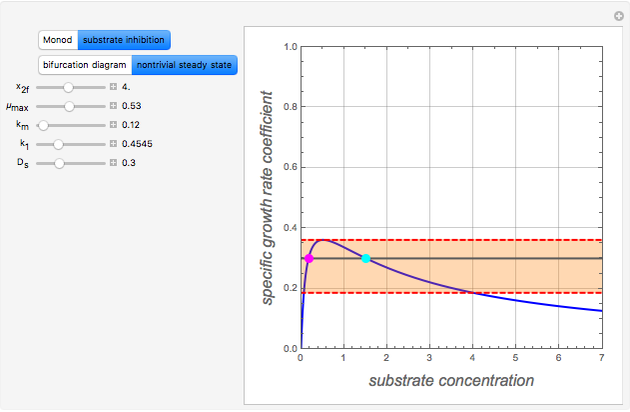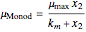
The specific growth coefficient with the substrate inhibition 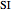is given by

.

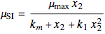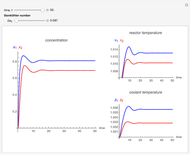
The biochemical reactor is governed by two coupled equations

,

,

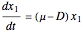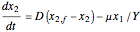where 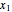is the biomass concentration, 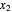is the substrate concentration, 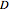is the dilution rate, is the yield, is the feed substrate concentration, and is the specific growth coefficient.

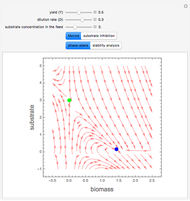
The steady states are the solutions of the following system of equations:

,

.

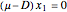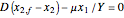The trivial solution is obtained for and 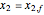. This corresponds to a situation where there are no cells left in the reactor, a phenomena called wash out.

The nontrivial solution is obtained if 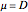and .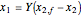

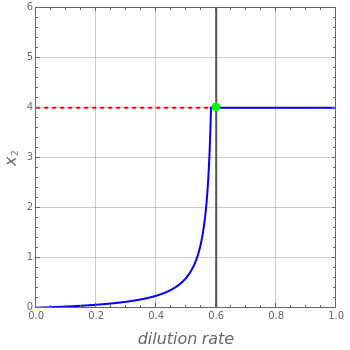
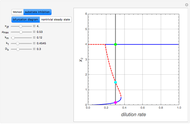
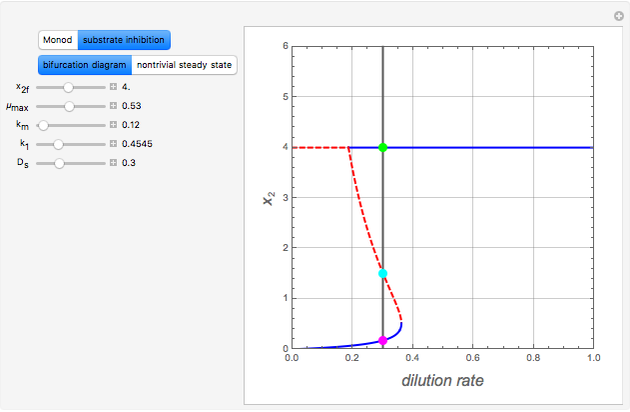
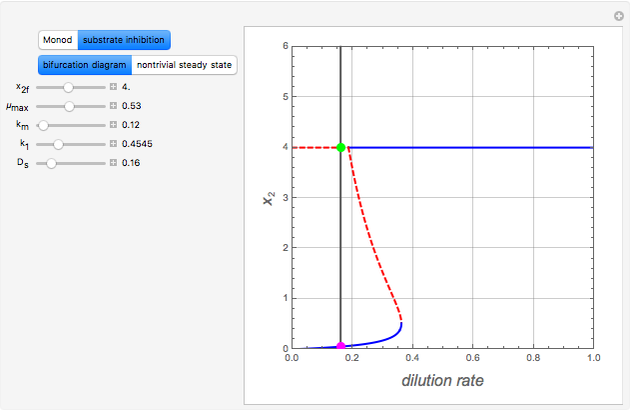
This Demonstration finds the nontrivial steady states and shows the bifurcation diagram (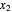 versus the bifurcation parameter ).

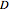For the Monod case there is a single nontrivial steady state if 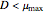. This steady state is stable. On the other hand, the trivial steady state is either stable (when 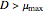) or unstable ().

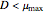For the 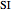model, there are two nontrivial steady states if the value of 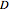is in the pink region (click "nontrivial steady state"). In that case, the following inequalities hold: 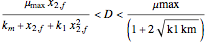. The magenta dot (low value of 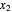) is stable because . The cyan dot (intermediate value of 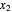) is unstable (a saddle point) because 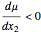. The trivial solution is either stable (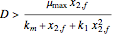) or unstable (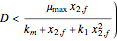). If 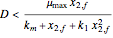, there is only one nontrivial steady state indicated by the magenta dot (low value of 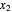). This steady state is stable because . 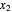The other value of verifies , thus 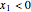(i.e., this solution is not feasible). Finally, if 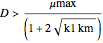, nontrivial solutions are not possible.