Polya Conjecture

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
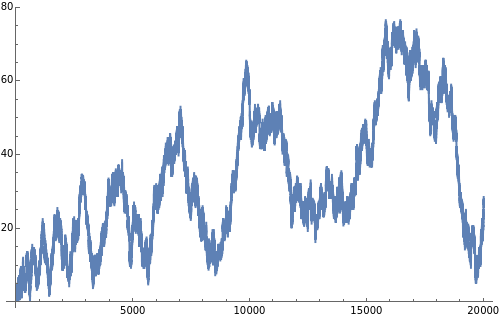
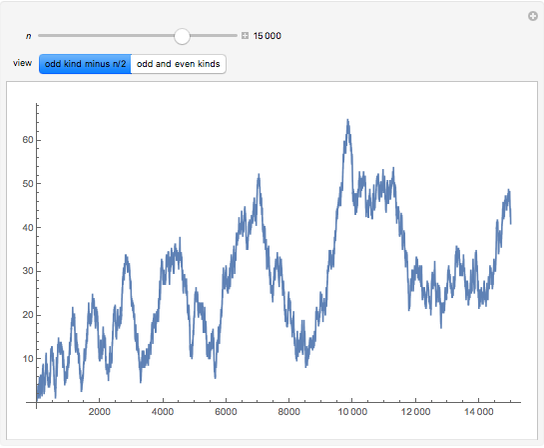
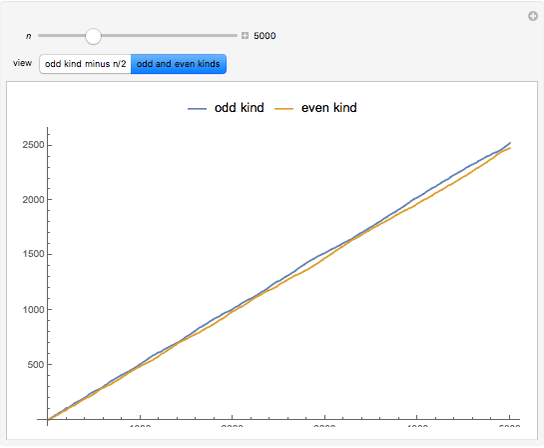
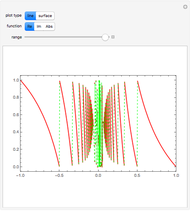
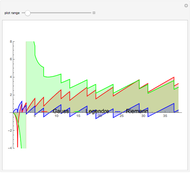
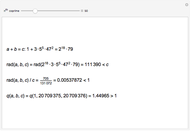
Define a number as of odd kind if the number of its prime factors is odd (taking multiplicity into account), and to be of even kind if the number of prime factors is even. Let  and
and  be the sum of the numbers of integers less than or equal to
be the sum of the numbers of integers less than or equal to  of the even and odd kinds.
of the even and odd kinds.
Contributed by: Enrique Zeleny (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Matt. "Examples of Apparent Patterns That Eventually Fail." Mathematics StackExchange. (Aug 27, 2014) math.stackexchange.com/questions/111440/examples-of-apparent-%5 Cpatterns-that-eventually-fail.
Permanent Citation