Reversible Steady-State Voltammograms at Microelectrodes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
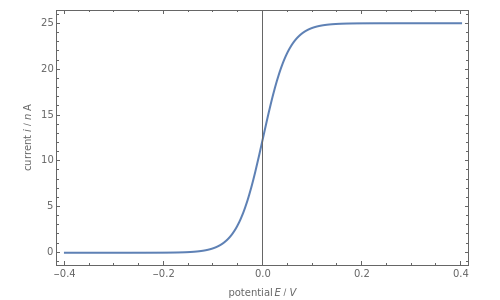
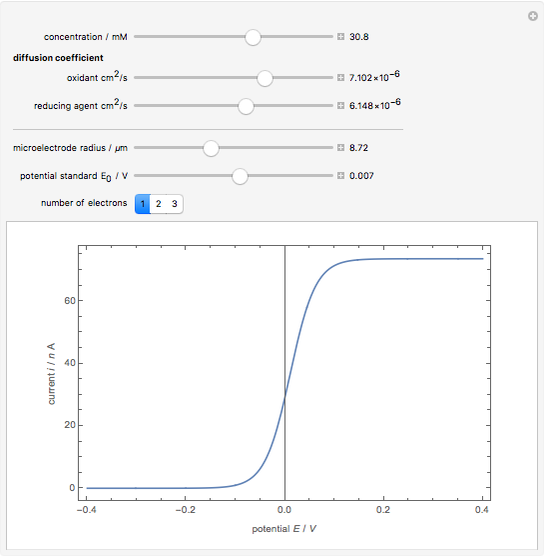
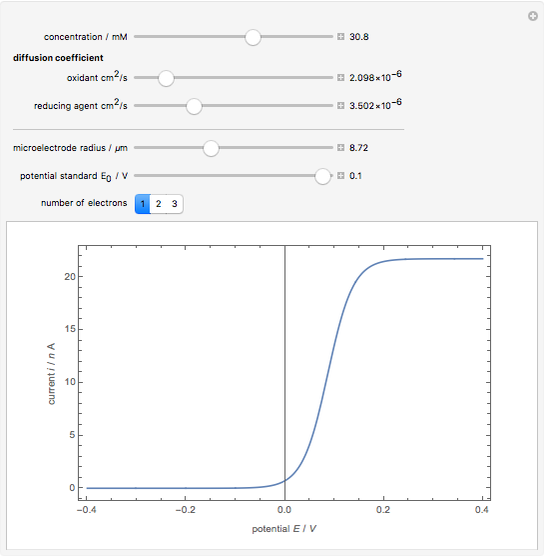
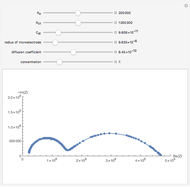
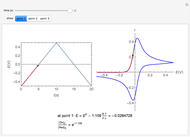
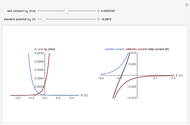
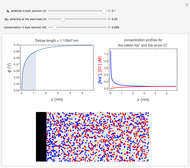
Cyclic voltammetry is one of the principal techniques in electrochemistry. This Demonstration shows a simulation of cyclic voltammetry on a microelectrode in steady state and with reversible kinetics.
Contributed by: Quang-Dao Trinh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
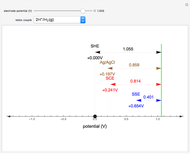
At the microelectrode, the redox reaction occurs: 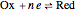 . Because the microelectrode is very small, the steady state is quickly attained. If the standard rate constant of the reaction redox on the microelectrode is very rapid (
. Because the microelectrode is very small, the steady state is quickly attained. If the standard rate constant of the reaction redox on the microelectrode is very rapid ( ), we have a reversible voltammogram.
), we have a reversible voltammogram.
According to [1], the reversible steady-state voltammogram satisfies the equation 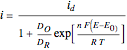 , where
, where 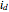 is the limiting current of the microelectrode,
is the limiting current of the microelectrode,  ,
, 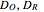 (
( ) is the diffusion coefficient of the oxidant and reducer,
) is the diffusion coefficient of the oxidant and reducer,  (
( m) is the radius of the microelectrode,
m) is the radius of the microelectrode, 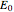 (V) is the standard potential of reaction redox,
(V) is the standard potential of reaction redox,  (V) is the applied potential,
(V) is the applied potential, 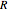 is the gas constant
is the gas constant 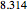
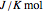 ,
, 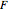 is the Faraday constant
is the Faraday constant 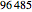 (C/mol), C (mol/L) is the concentration of oxidant,
(C/mol), C (mol/L) is the concentration of oxidant, 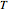 (K) is the temperature, and
(K) is the temperature, and  is the number of electrons transferred.
is the number of electrons transferred.
[1] A. M. Bond, K. B. Oldham, and C. G. Zoski, "Theory of Electrochemical Processes at an Inlaid Disc Microelectrode under Steady-State Conditions," J. Electroanal. Chem., 245(1–2), 1988 p. 71.
Permanent Citation