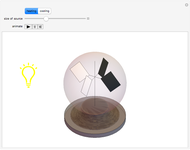
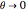Feynman's Wobbling Plate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In his eccentric collection of autobiographical stories (see reference), Richard Feynman recounts: "I was in the cafeteria and some guy, fooling around, throws a plate in the air. As the plate went up in the air I saw it wobble, and I noticed the red medallion of Cornell on the plate going around. It was pretty obvious to me that the medallion went around faster than the wobbling. I had nothing to do, so I start figuring out the motion of the rotating plate. I discovered that when the angle is very slight, the medallion rotates twice as fast as the wobble rate—two to one. It came out of a complicated equation! I went on to work out equations for wobbles. Then I thought about how the electron orbits start to move in relativity. Then there's the Dirac equation in electrodynamics. And then quantum electrodynamics. And before I knew it… the whole business that I got the Nobel prize for came from that piddling around with the wobbling plate." A replica of the Cornell plate is now part of an exhibit marking the centennial of the Nobel Prize.
[more]
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
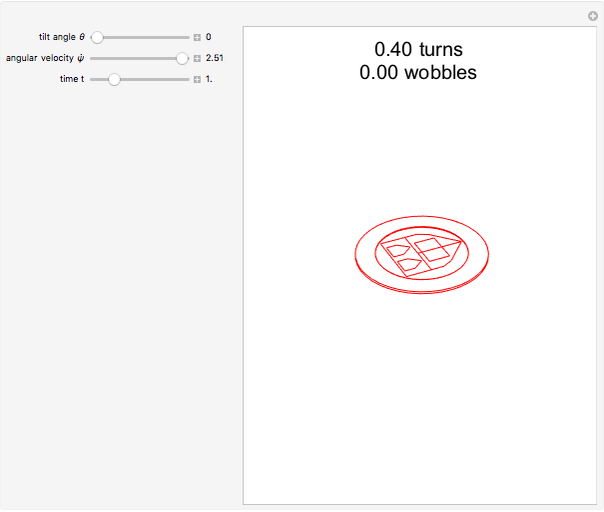
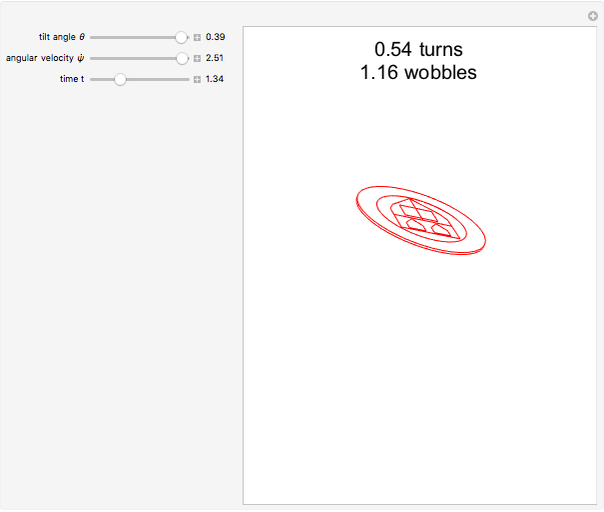
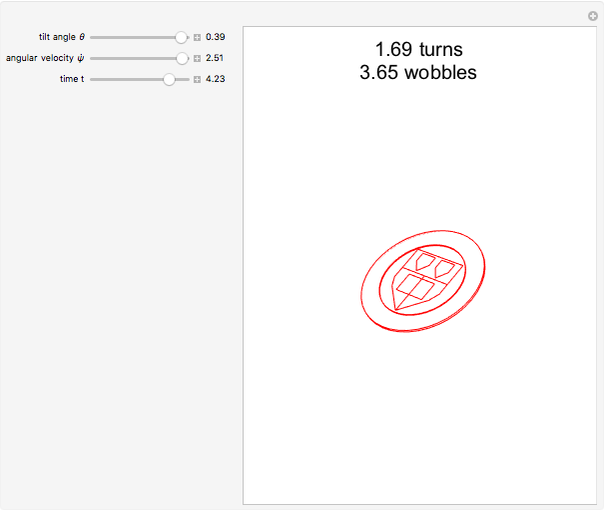
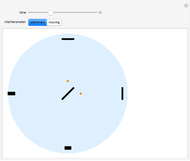
Snapshots
Details
Euler's equations for free rotation of a rigid body are given by 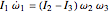 ;
; 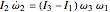 ;
; 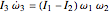 . For a circular disk of radius
. For a circular disk of radius 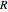 , mass
, mass 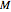 and negligible thickness, the principal moments of inertia are
and negligible thickness, the principal moments of inertia are 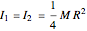 ,
, 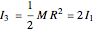 . The third Euler equation reduces to
. The third Euler equation reduces to  . Thus
. Thus 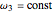 . This is the angular velocity of the plate about its axis of symmetry, and is taken as one of the initial conditions. The first two Euler equations are then satisfied by
. This is the angular velocity of the plate about its axis of symmetry, and is taken as one of the initial conditions. The first two Euler equations are then satisfied by 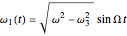 ,
, 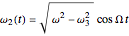 , where
, where 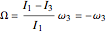 . The motion of the rigid body in the space-fixed frame can be expressed in terms of the Euler angles
. The motion of the rigid body in the space-fixed frame can be expressed in terms of the Euler angles 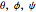 , using the relations
, using the relations  ,
, 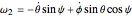 ,
,  . If the axis of the plate is initially inclined by an angle
. If the axis of the plate is initially inclined by an angle  from the vertical, with an angular velocity
from the vertical, with an angular velocity 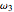 , then the motion of the plate is given by
, then the motion of the plate is given by 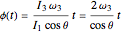 ,
, 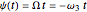 ,
,  . The rotation of the plate is represented by
. The rotation of the plate is represented by 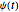 , while its precession or "wobbling" is given by
, while its precession or "wobbling" is given by  . As
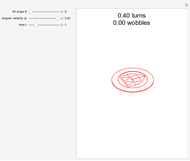
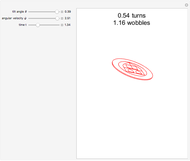
. As  approaches 0, the wobbling frequency approaches twice the rotation frequency, but the wobbling amplitude also decreases.
approaches 0, the wobbling frequency approaches twice the rotation frequency, but the wobbling amplitude also decreases.
References:
R. P. Feynman, Surely You're Joking, Mr. Feynman!, New York: W. W. Norton, 1985 pp. 157–158.
H. Goldstein, Classical Mechanics, Cambridge, MA: Addison-Wesley, 1953.
Permanent Citation