Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Scrambler Ride

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

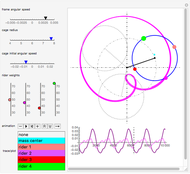
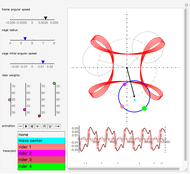
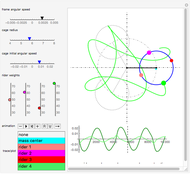
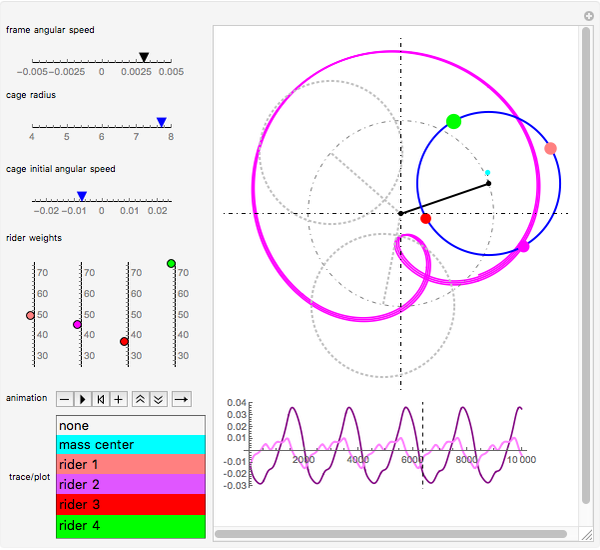
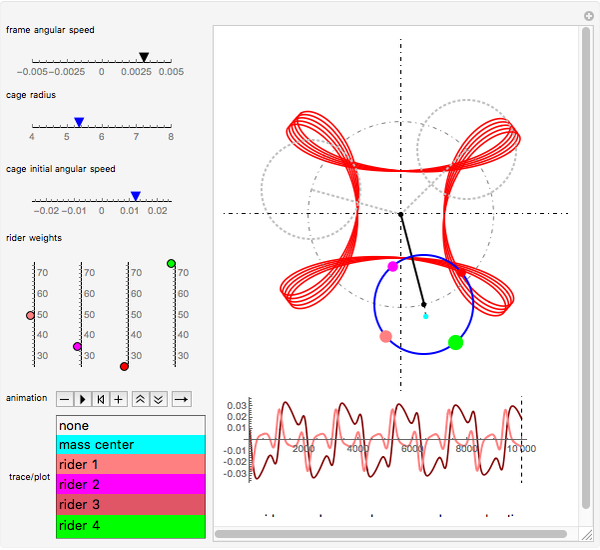
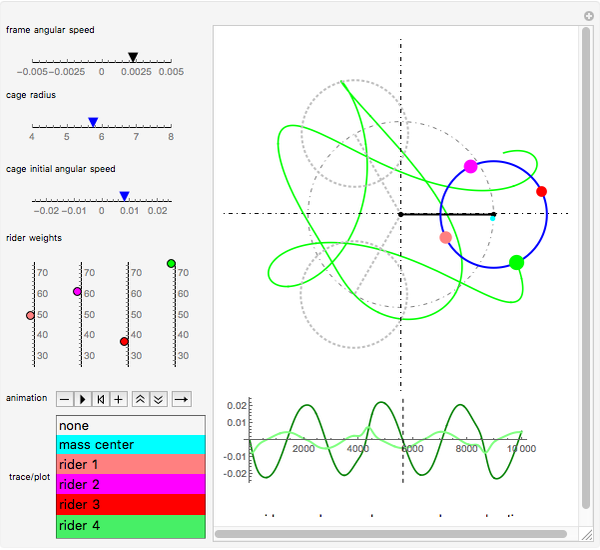
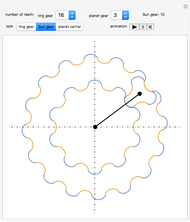
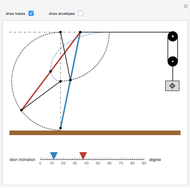
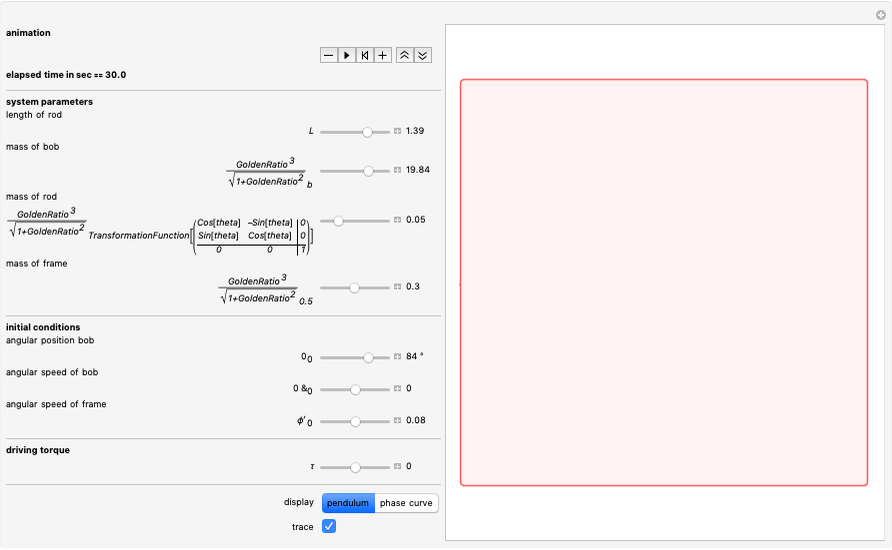
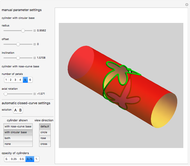
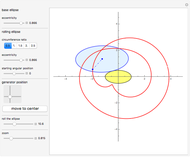
The scrambler (or twist) is a popular amusement park ride. It turns on a dual axis, with each axis a center of an independent rotation. A frame with three arms rotates at constant speed around a central axis. At the end of each arm, a second axis is the center of a rotating cage containing four riders.

[more]

In the real world, the cage and the frame rotate in opposite directions, giving the riders the impression of crashing into each other. In this Demonstration, the frame is rotating at a constant angular speed while the cage is only given an initial speed and is left freewheeling the rest of the time.

[less]

Contributed by: Erik Mahieu (January 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The scrambler has two degrees of freedom: the rotation of the frame and the rotation of the cages relative to the frame.

The weights of the four riders determine the position of the center of mass for each cage. This position governs the movement of the cage.

The equations of motion are similar to the ones for the double pendulum: 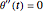, , 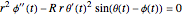where 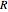is the length of a frame arm, is the radius of the cage, is the angular position of the arm of the frame, and is the angular position of the cage.

The math and physics of amusement rides can be found in [1]. For a drawing from the original 1940 patent of this ride, see [2].

References

[1] Nathan A. Unterman, Amusement Park Physics: A Teacher's Guide, 2nd ed., Portland, ME: Walch Publishing, 2001. books.google.com/books?id=xT5ooXBhEG4C.

[2] D. Burton. "Richard Harris' 1940 History-Making Patent." www.ride-extravaganza.com/intermediate/scrambler/merry-go-round.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send