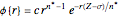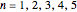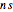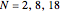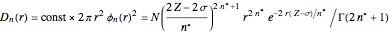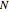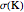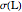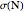Shell Structure of Noble Gas Atoms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
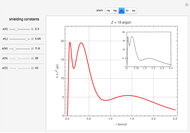
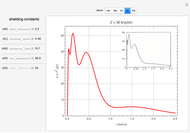
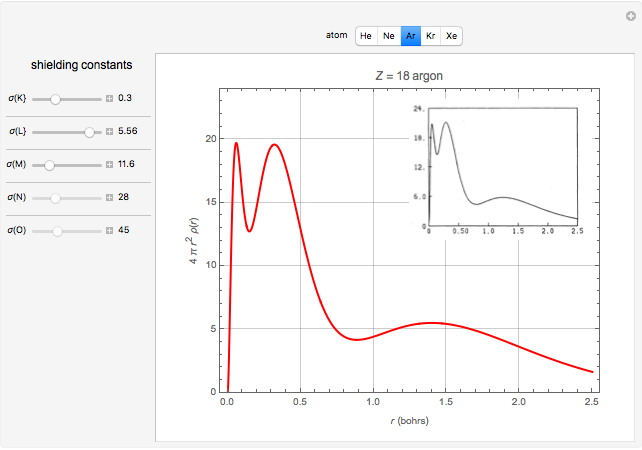
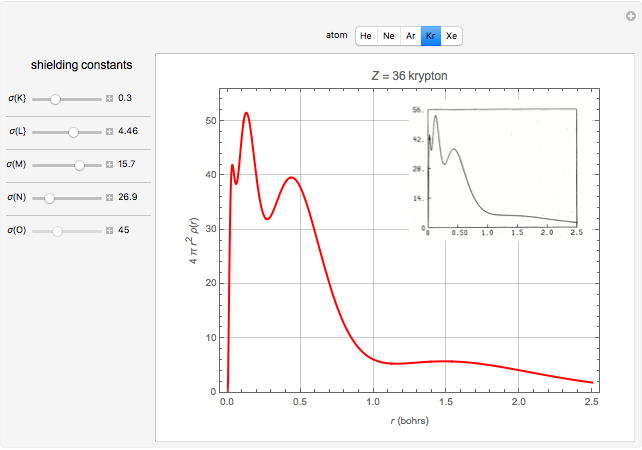
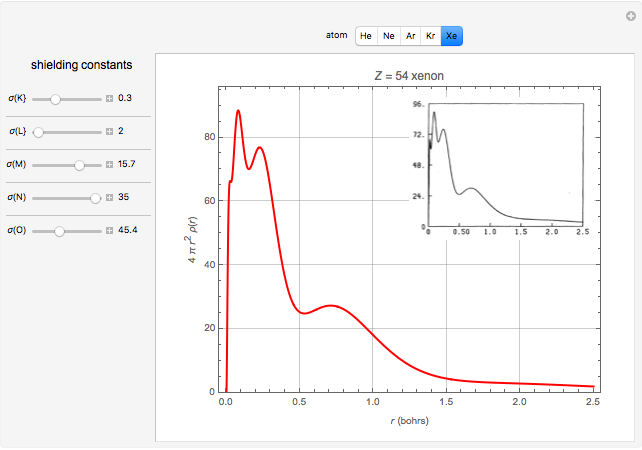
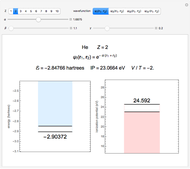
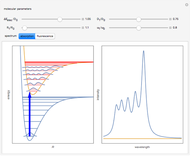
Accurate Hartree–Fock computations were carried out long ago on all the atoms in the periodic table [1]. From these results, Wang and Parr [2] have plotted radial distribution functions (RDFs) 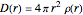 , where
, where  is the total electron density, for the noble gas atoms He (
is the total electron density, for the noble gas atoms He (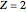 ), Ne (
), Ne ( ), Ar (
), Ar (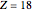 ), Kr (
), Kr (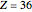 ), and Xe (
), and Xe ( ). These are shown as insets in the graphics. The shell structure of the electron distributions is evident, and can be identified with the K, L, M, N, and O shells, corresponding to principal quantum numbers 1 to 5, respectively.
). These are shown as insets in the graphics. The shell structure of the electron distributions is evident, and can be identified with the K, L, M, N, and O shells, corresponding to principal quantum numbers 1 to 5, respectively.
Contributed by: S. M. Blinder (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] E. Clementi, "Tables of Atomic Functions," IBM Journal of Research and Development, 9(1), 1965 pp. 87–89. doi:10.1147/JRD.1965.5392159.
[2] W.-P. Wang and R. G. Parr, "Statistical Atomic Models with Piecewise Exponentially Decaying Electron Densities," Physical Review A, 16(3), 1977 pp. 891–902.doi:10.1103/PhysRevA.16.891.
[3] Wikipedia. "Slater's Rules." (Apr 15, 2014) en.wikipedia.org/wiki/Slater's_rules.
Permanent Citation