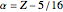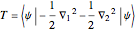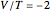Two-Parameter Variational Functions for the Helium Isoelectronic Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
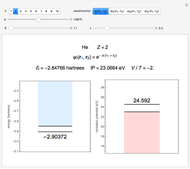
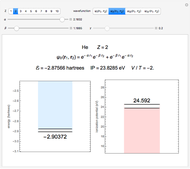
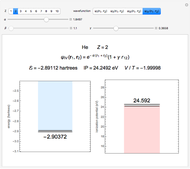
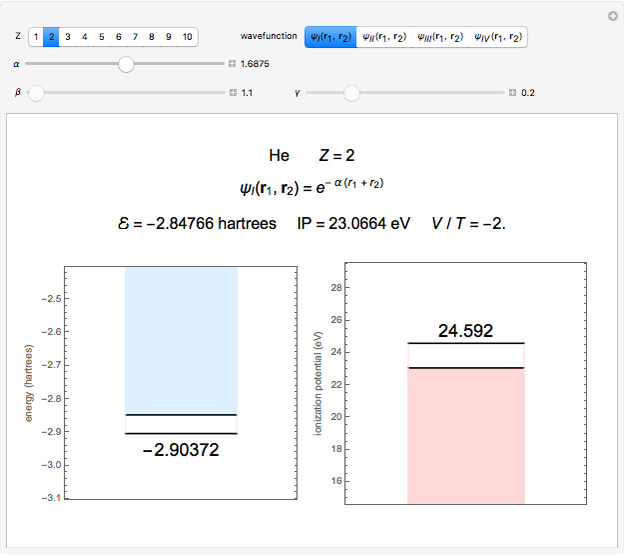
The simple variational treatment of the helium atom and, more generally, the related series of isoelectronic ions, is a standard topic in quantum chemistry texts. The Hamiltonian for helium-like systems is given by  , expressed in atomic units
, expressed in atomic units  , assuming infinite nuclear mass and neglecting relativistic corrections. Atomic numbers
, assuming infinite nuclear mass and neglecting relativistic corrections. Atomic numbers  from 1 (
from 1 (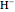 ) and 2 (
) and 2 ( ) through 10 (
) through 10 (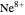 ) are considered here. Unlike the one-electron Schrödinger equation, this two-electron problem
) are considered here. Unlike the one-electron Schrödinger equation, this two-electron problem  cannot be solved analytically. E. A. Hylleraas, around 1930, carried out variational calculations giving ground state energies and ionization potentials in essential agreement with experimental results (see the Demonstration "Variational Calculations on the Helium Isoelectronic Series"). This, at least to physicists and chemists, could be considered a "proof" of the general validity of the Schrödinger equation. (In contrast, the Bohr theory gave correct energies for the hydrogen atom but failed miserably for helium and heavier atoms.)
cannot be solved analytically. E. A. Hylleraas, around 1930, carried out variational calculations giving ground state energies and ionization potentials in essential agreement with experimental results (see the Demonstration "Variational Calculations on the Helium Isoelectronic Series"). This, at least to physicists and chemists, could be considered a "proof" of the general validity of the Schrödinger equation. (In contrast, the Bohr theory gave correct energies for the hydrogen atom but failed miserably for helium and heavier atoms.)
Contributed by: Wai-Kee Li and S. M. Blinder (April 2012)
(Chinese University of Hong Kong)
Open content licensed under CC BY-NC-SA
Snapshots
Details
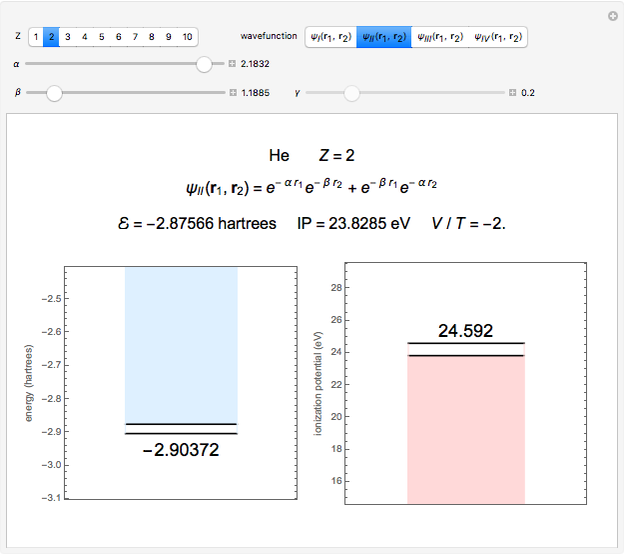
Snapshot 1: optimized one-parameter function for helium
Snapshot 2: optimized open-shell function
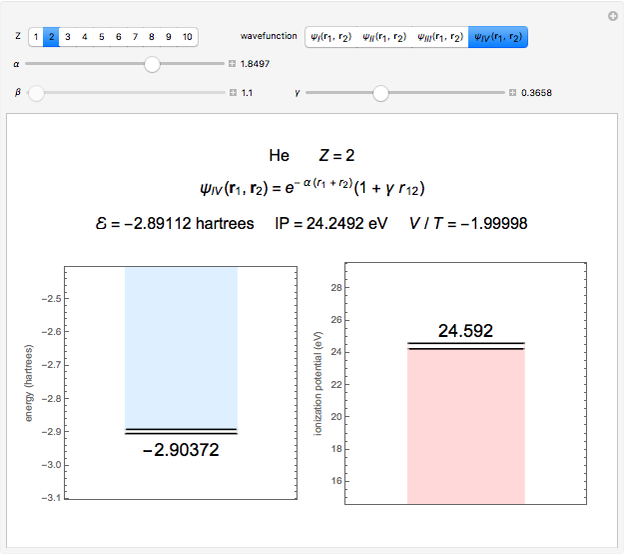
Snapshot 3: best approximate helium function in this Demonstration
Snapshot 4: simple result for neon; higher values of  make electron repulsion less significant
make electron repulsion less significant
Snapshot 5: simplest function for hydride ion 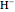 ; implies dissociation to H +
; implies dissociation to H + 
Snapshot 6: open-shell function; shows existence of weakly-bound 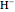
References
[1] W.-K. Li, G.-D. Zhou, and T. Mak, Advanced Structural Inorganic Chemistry, Oxford: University Press, 2008, pp. 46–48.
[2] W.-K. Li, "Two-Parameter Wave Function for the Helium Sequence," Journal of Chemical Education, 64(2), 1987 pp. 128–129.
[3] W.-K. Li, "A Lesser Known One-Parameter Wave Function for the Helium Sequence and the Virial Theorem," Journal of Chemical Education, 65(11), 1988 pp. 963–964.
[4] K. L. Liu and W.-K. Li, "The Simple Variational Wavefunctions for the Helium Atom and the Virial Theorem," American Journal of Physics, 58(12), 1990 pp. 1202–1203.
Permanent Citation