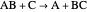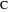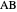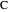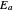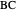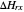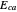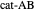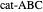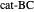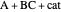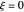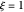Simple Arrhenius Model for Activation Energy and Catalysis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
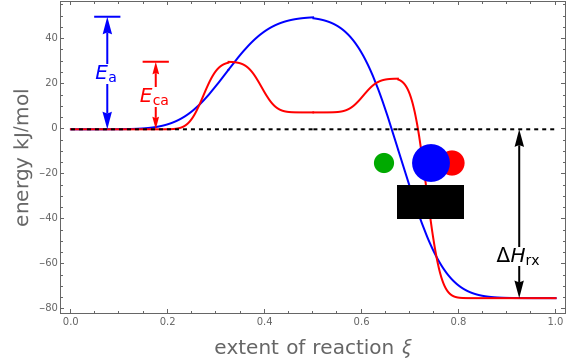
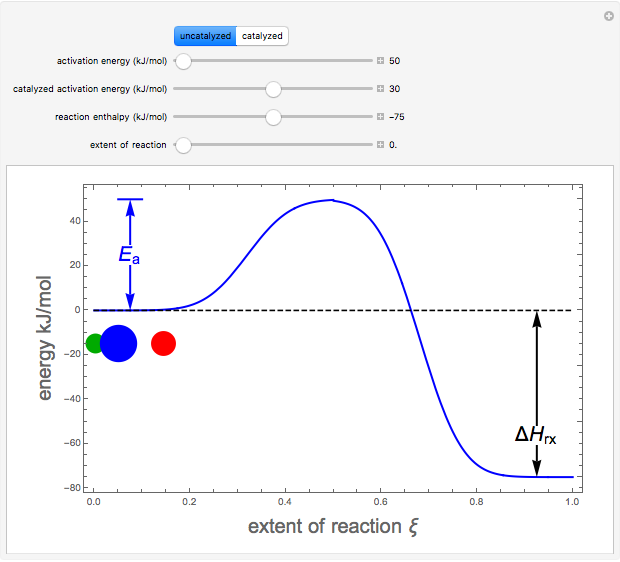
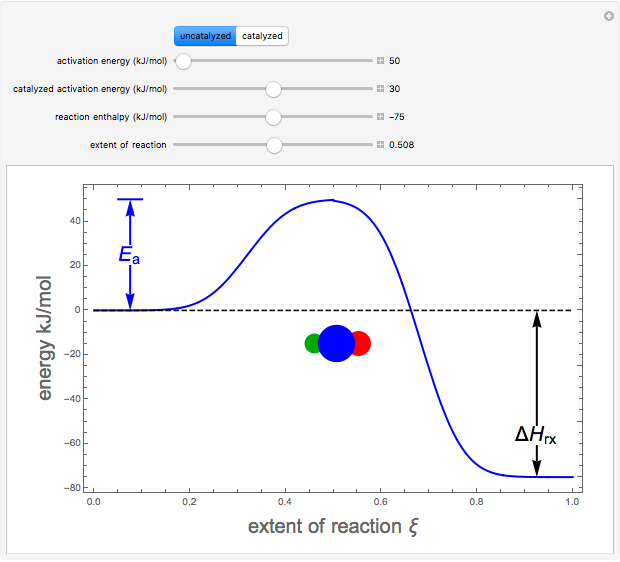
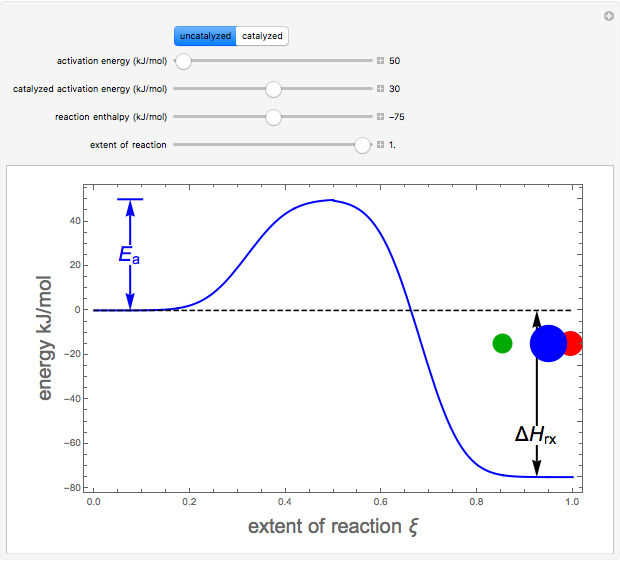
The concept of activation energy was introduced by Svante Arrhenius in 1889. In order for a chemical reaction to occur, even one which is thermodynamically favorable—with a negative enthalpy of reaction  —
— an energy of magnitude greater than or equal to
an energy of magnitude greater than or equal to 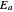 , known as the activation energy, must be supplied to overcome a barrier. This is usually accomplished by heating the reaction mixture. The most rudimentary form of the Arrhenius equation, for the rate constant of the forward reaction, is given by
, known as the activation energy, must be supplied to overcome a barrier. This is usually accomplished by heating the reaction mixture. The most rudimentary form of the Arrhenius equation, for the rate constant of the forward reaction, is given by  . Clearly, the rate is increased at higher temperature
. Clearly, the rate is increased at higher temperature 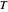 . More advanced versions of the Arrhenius equation, which we do not consider here, take into account possible temperature dependence of the frequency factor
. More advanced versions of the Arrhenius equation, which we do not consider here, take into account possible temperature dependence of the frequency factor 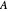 , and even of the activation energy
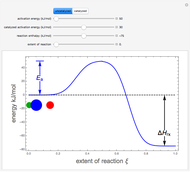
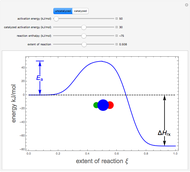
, and even of the activation energy 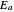 itself. There are also modifications dependent on the molecularity (bimolecular etc.) of the reaction. Near the peak of the activation curve, the reacting system goes through a short-lived intermediate state, which can be written as
itself. There are also modifications dependent on the molecularity (bimolecular etc.) of the reaction. Near the peak of the activation curve, the reacting system goes through a short-lived intermediate state, which can be written as 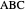 . In some theoretical treatments, this is known as an "activated complex".
. In some theoretical treatments, this is known as an "activated complex".
Contributed by: S. M. Blinder (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
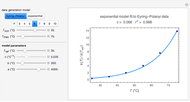
An old rule of thumb in chemistry claims that increasing the temperature by 10°C doubles the rate of a reaction. A simple calculation using the Arrhenius equation  shows that, for an activation energy around 50 kJ/mol, increasing
shows that, for an activation energy around 50 kJ/mol, increasing 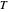 from, say, 300K to 310K approximately doubles
from, say, 300K to 310K approximately doubles  .
.
Snapshots 1–3: idealized molecular pathway of an uncatalyzed chemical reaction
Snapshots 4–6: possible sequence for a chemical reaction involving a catalyst
References
[1] Wikipedia. "Activation Energy." (May 26, 2012) en.wikipedia.org/wiki/Activation_energy.
[2] Wikipedia. "Catalysis." (May 26, 2012) en.wikipedia.org/wiki/Catalyst.
Permanent Citation