Idealized Belousov-Zhabotinsky Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
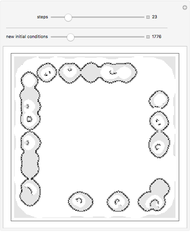
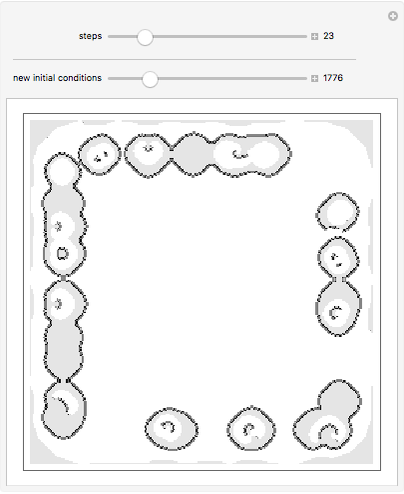
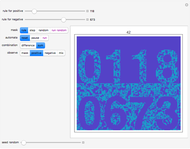
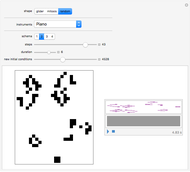
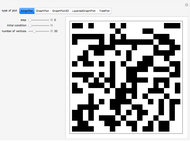
This Demonstration shows an idealized version of the Belousov-Zhabotinsky reaction implemented by means of a two-dimensional, totalistic cellular automaton.
Contributed by: Luca Zammataro (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
NKS can describe self-organization of complex chemical and biological spatial structures. Sometimes some of these structures can share the same pattern. For instance, spiral waves—studied in the past by Arthur Winfree and others—are typical of many chemical reactions, as well as in slime mold colonies. This pattern is also typical of the amoeba Dictyostelium discoideum, in which spiral structures arise from the movements of amoebae in response to propagating waves of the cAMP.
In this Demonstration, the Belousov-Zhabotinsky chemical reaction pattern is implemented by means of two-dimensional totalistic cellular automaton. This Demonstration uses a range 1, 20-color totalistic cellular automaton with rule number 1350851716507335422, but a wide number of rules around this one produce similar patterns.
Observing the pattern formation, two different spatial structures can arise: concentric waves and spiral waves. The two different patterns depend on the initial conditions and represent a clear example of multiple modes of self-organization.
For further information, see:
R. Solé and B. Goodwin, Signs of Life: How Complexity Pervades Biology, New York: Basic Books, 2000.
S. Kauffman, At Home in the Universe: The Search for the Laws of Self-Organization and Complexity, Oxford: Oxford University Press, 1995.
Belousov-Zhabotinsky reaction on Wikipedia
CA simulator Cellab, by Rudy Rucker and John Walker (rule ZHABO.JC)
A. Winfree, When Time Breaks Down: The Three-Dimensional Dynamics of Electrochemical Waves and Cardiac Arrhythmias, Princeton: Princeton University Press, 1987.
Permanent Citation
"Idealized Belousov-Zhabotinsky Reaction"
http://demonstrations.wolfram.com/IdealizedBelousovZhabotinskyReaction/
Wolfram Demonstrations Project
Published: March 7 2011