Triple Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
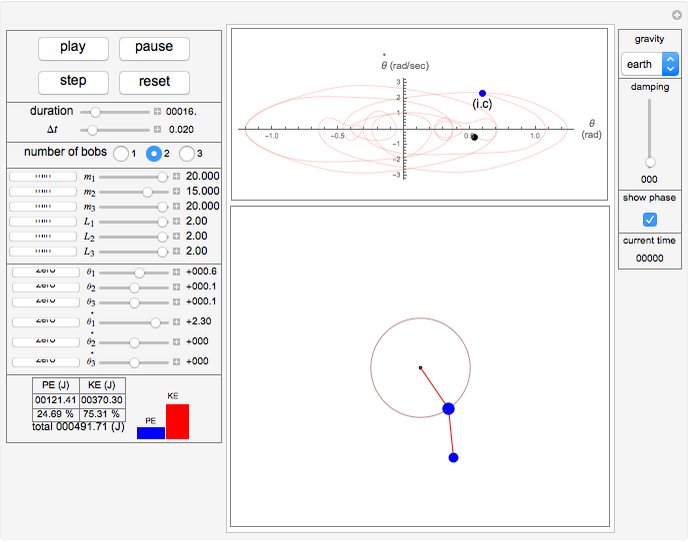
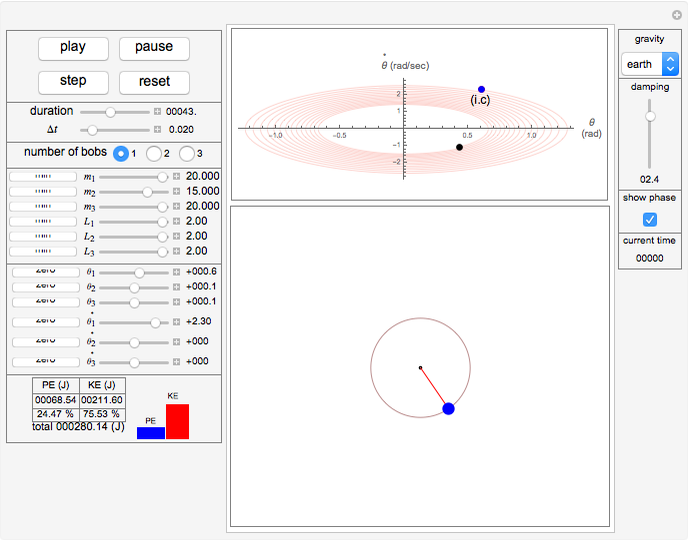
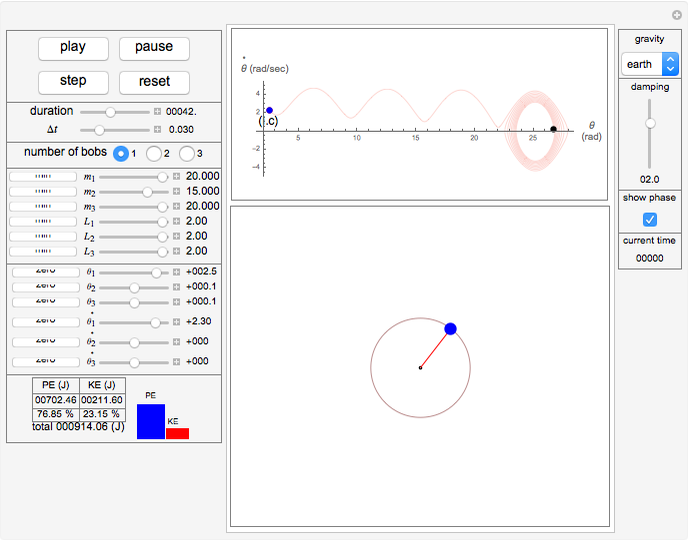
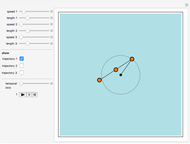
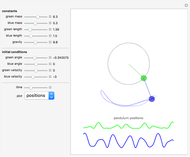
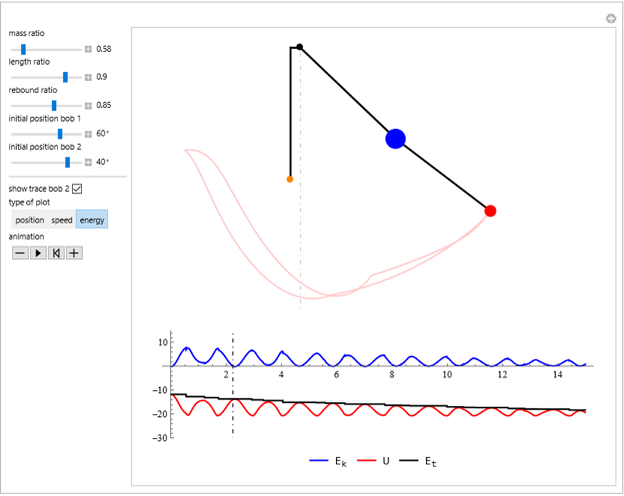
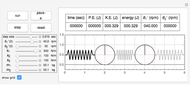
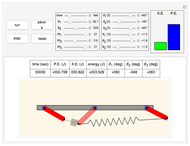
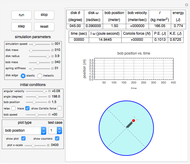
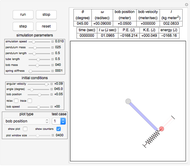
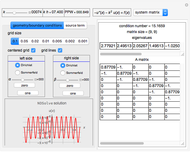
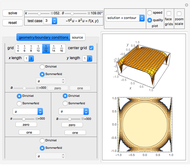
This Demonstration simulates the motion of a free moving damped triple pendulum. It can also be reduced to a simple or double pendulum since the number of bobs is a configurable parameter. Viscous damping is due to the pendulums moving in fluid. The phase portrait diagram is updated during simulation. The energy of the system is displayed as the simulation is running and is seen to be constant as expected when damping is not present. Initial conditions for the positions of the pendulum bobs can be adjusted either using the mouse (by dragging a bob to a new location) or by using the control sliders.
[more]
Contributed by: Nasser M. Abbasi (October 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equations of motion of the pendulum were derived using the Lagrangian method. For the  -bob pendulum, there are
-bob pendulum, there are  second-order nonlinear differential equations and
second-order nonlinear differential equations and  degrees of freedom. The equations are kept in their nonlinear form since NDSolve was used for solving them. Mathematica was used to do the analytical derivation due to the high complexity of algebra for the
degrees of freedom. The equations are kept in their nonlinear form since NDSolve was used for solving them. Mathematica was used to do the analytical derivation due to the high complexity of algebra for the  case.
case.
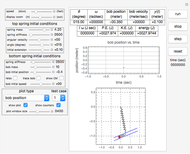
Initial position conditions can be changed by dragging the bob using the mouse. When you click in the display, there is a pause and then the mouse can be used to drag the bob to a new location. Logic inside the Demonstration detects which bob to drag based on the proximity of the current mouse location to known bob positions.
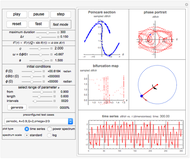
The top buttons labeled "play", "pause", "step", and "reset" are self-explanatory and used to control the simulation. The control labeled "duration" is used to set the maximum simulation time. When this time is reached, the simulation will restart from  automatically. The control labeled "
automatically. The control labeled "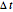 " is used to change the time step for the display. The smaller the time step, the more accurate the simulation, but it takes longer to complete.
" is used to change the time step for the display. The smaller the time step, the more accurate the simulation, but it takes longer to complete.
The control labeled "number of bobs" is used to change the pendulum type to 1, 2, or 3 (simple, double, or triple). The controls below that are used to adjust the mass of the bobs, with units in 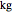 . All units in this simulation are in SI units. The controls below that are used to change the length of each pendulum bar.
. All units in this simulation are in SI units. The controls below that are used to change the length of each pendulum bar.
The controls below that are used to set the initial conditions. Units are in radians for the angles and in radians per second for the angular velocities. The initial angle positions can also be set using the mouse as mentioned above; however, using the controls can provide more accurate settings if needed. For convenience, small buttons next to the control variables can be used to quickly set the value to zero.
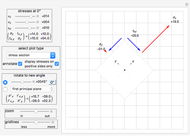
The "gravity" control is used to select the gravitational constant  . The control labeled "show phase" is used to turn the phase portrait plot on and off. The red point in the phase portrait plot indicates the initial conditions, and the black point is the position at the end of the duration. The moving blue point is the position in phase space at the current time.
. The control labeled "show phase" is used to turn the phase portrait plot on and off. The red point in the phase portrait plot indicates the initial conditions, and the black point is the position at the end of the duration. The moving blue point is the position in phase space at the current time.
The control labeled "damping" is used to change the damping coefficient. At the bottom is a display of the energy plot, which shows the current kinetic energy (KE), potential energy (PE), and the total energy in Joules.
The angles 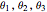 are all measured from the vertical line. When the pendulum is hanging vertically at rest, then all angles will have zero values at this position. The angles and velocities are taken to be positive in the counterclockwise direction.
are all measured from the vertical line. When the pendulum is hanging vertically at rest, then all angles will have zero values at this position. The angles and velocities are taken to be positive in the counterclockwise direction.
Reference
[1] D. A. Wells, Schaum's Lagrangian Dynamics, New York: McGraw-Hill, 1967.
Permanent Citation