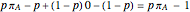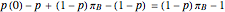Sports Arbitrage: Two-Agency, Two-Outcome Efficient Pricing Test

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
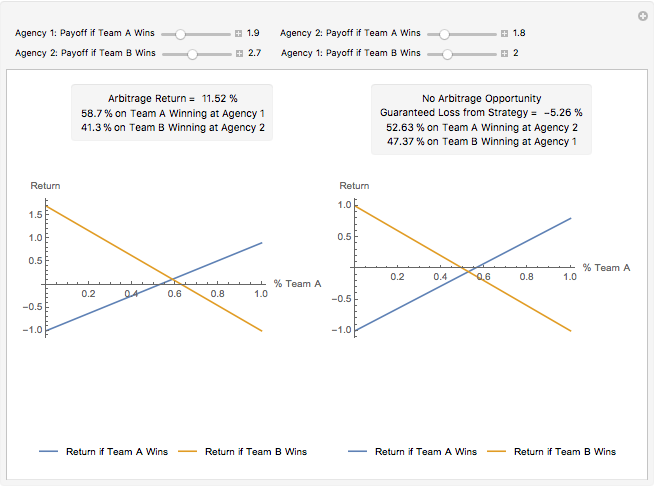
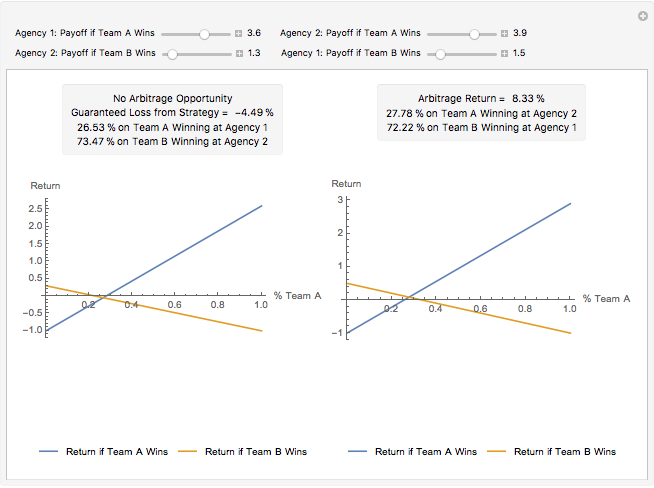
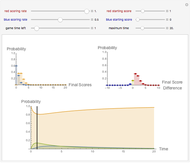
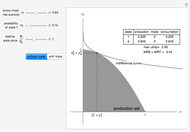
This Demonstration shows the opportunity that may be created if betting agencies do not agree on the odds of a match with two teams and no possibility for a draw. The graphs represent the payoffs of possible weighted portfolios of the two outcomes. The  axis represents the proportion
axis represents the proportion  of any bet in the portfolio on team A winning. If
of any bet in the portfolio on team A winning. If  , then the agent (bet placer) believes team B will win the game. If odds at the agency where the bet was placed are
, then the agent (bet placer) believes team B will win the game. If odds at the agency where the bet was placed are  that team B will win, the bet placer will receive the payoff from the agency minus their initial investment, making their return
that team B will win, the bet placer will receive the payoff from the agency minus their initial investment, making their return  if B does win. If B does not win, they will lose their initial investment (
if B does win. If B does not win, they will lose their initial investment ( ). Let
). Let 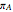 and
and 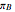 be the payoff from A winning and the payoff from B winning, respectively. The profit functions for a weighted portfolio of outcomes are therefore:
be the payoff from A winning and the payoff from B winning, respectively. The profit functions for a weighted portfolio of outcomes are therefore:
Contributed by: Tom Stannard (May 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] E. Franck, E. Verbeek, and S. Nüesch, "Inter-market Arbitrage in Betting," Economica, 80(318), 2013 pp. 300–325. doi:10.1111/ecca.12009.
[2] B. R. Marshall, "How Quickly Is Temporary Market Inefficiency Removed?," The Quarterly Review of Economics and Finance, 49(3), 2009 pp. 917–930. doi:10.1016/j.qref.2009.04.006.
Permanent Citation