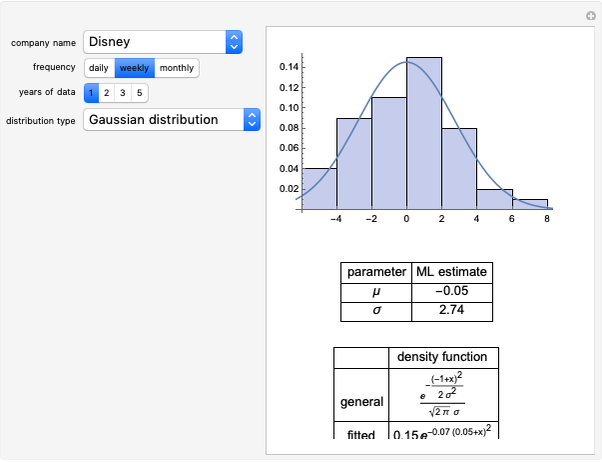
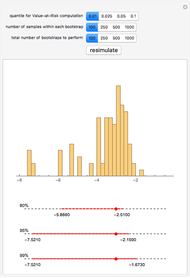
Linear Dependence between Two Bernoulli Random Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Pearson correlation coefficient, denoted  , is a measure of the linear dependence between two random variables, that is, the extent to which a random variable
, is a measure of the linear dependence between two random variables, that is, the extent to which a random variable 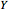 can be written as
can be written as 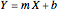 , for some
, for some  and some
and some  . This Demonstration explores the following question: what correlation coefficients are possible for a random vector
. This Demonstration explores the following question: what correlation coefficients are possible for a random vector 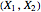 , where
, where 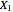 is a Bernoulli random variable with parameter
is a Bernoulli random variable with parameter 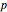 and
and 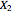 is a Bernoulli random variable with parameter
is a Bernoulli random variable with parameter  ? Interestingly, a two-dimensional Bernoulli random vector has a correlation coefficient that is constrained by the choices of
? Interestingly, a two-dimensional Bernoulli random vector has a correlation coefficient that is constrained by the choices of 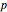 and
and  .
.
Contributed by: Jeff Hamrick (August 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the sake of simplicity, you are constrained to choose 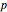 and
and  that are slightly bounded away from 0 and 1.
that are slightly bounded away from 0 and 1.
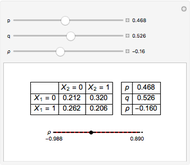
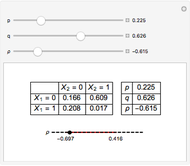
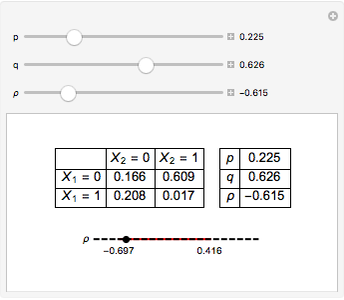
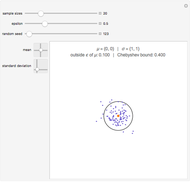
In the upper left-hand corner, there is a possible joint distribution of 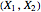 that accommodates your choices of
that accommodates your choices of 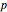 ,
,  , and
, and  . Additionally, at the bottom is shown (with a red line) the linear correlation coefficients that are attainable for fixed choices of
. Additionally, at the bottom is shown (with a red line) the linear correlation coefficients that are attainable for fixed choices of 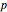 and
and  . The basic lesson is clear: it is not possible to couple together two arbitrary Bernoulli random variables in such a way that any conceivable linear correlation coefficient is attained. Notice that choosing
. The basic lesson is clear: it is not possible to couple together two arbitrary Bernoulli random variables in such a way that any conceivable linear correlation coefficient is attained. Notice that choosing 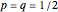 maximizes the range of possible values of
maximizes the range of possible values of  .
.
For a two-dimensional random vector 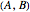 , where both
, where both 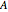 and
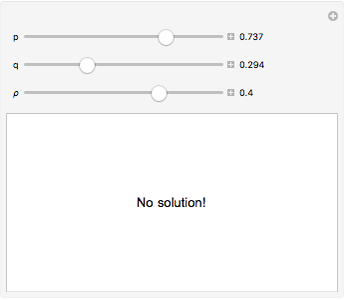
and 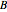 are discrete random variables, finding a joint probability distribution that triggers a particular linear correlation coefficient is equivalent to solving a system of linear equations. It is not surprising, then, that sometimes this system of linear equations has no solution, a unique solution, or infinitely many solutions.
are discrete random variables, finding a joint probability distribution that triggers a particular linear correlation coefficient is equivalent to solving a system of linear equations. It is not surprising, then, that sometimes this system of linear equations has no solution, a unique solution, or infinitely many solutions.
If in the  -dimensional random vector
-dimensional random vector 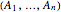 the
the 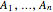 are Gaussian, then finding a joint probability distribution with a particular variance-covariance matrix (and, therefore, particular pairwise linear correlation coefficients between the coordinates of the
are Gaussian, then finding a joint probability distribution with a particular variance-covariance matrix (and, therefore, particular pairwise linear correlation coefficients between the coordinates of the  -dimensional random vector) also happens to be equivalent to solving a system of linear equations. This fact is true for any elliptical distribution as well, that is, a distribution with a density function whose constant curves are ellipsoids. In general, however, the dependence between two or more random variables cannot be captured by a single number.
-dimensional random vector) also happens to be equivalent to solving a system of linear equations. This fact is true for any elliptical distribution as well, that is, a distribution with a density function whose constant curves are ellipsoids. In general, however, the dependence between two or more random variables cannot be captured by a single number.
Permanent Citation