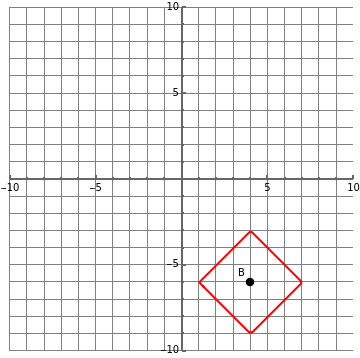
Taxicab Geometry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
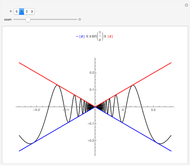
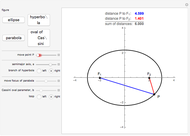
The traditional (Euclidean) distance between two points in the plane is computed using the Pythagorean theorem and has the familiar formula,  . In taxicab geometry, the distance is instead defined by
. In taxicab geometry, the distance is instead defined by  . This Demonstration allows you to explore the various shapes that circles, ellipses, hyperbolas, and parabolas have when using this distance formula. An option to overlay the corresponding Euclidean shapes is included for purposes of comparison.
. This Demonstration allows you to explore the various shapes that circles, ellipses, hyperbolas, and parabolas have when using this distance formula. An option to overlay the corresponding Euclidean shapes is included for purposes of comparison.
Contributed by: Marc Brodie (March 2011)
(Benedictine University at Mesa)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The seven possible points B serve as the center of the circle, the focus of the parabola, and one of the foci for the ellipse and hyperbola. (The other focus A is fixed at the origin.) The three lines  are the directrix when plotting a parabola. These choices for B and
are the directrix when plotting a parabola. These choices for B and  are inclusive enough to show all the interesting variations of shapes that can occur. The value
are inclusive enough to show all the interesting variations of shapes that can occur. The value  serves to vary the fixed distance in the locus of points definitions of the four figures. For those familiar with Krause's book, the "midset" can be displayed using
serves to vary the fixed distance in the locus of points definitions of the four figures. For those familiar with Krause's book, the "midset" can be displayed using  when plotting hyperbolas.
when plotting hyperbolas.
Snapshot 2 shows a degenerate ellipse. In Euclidean geometry,  is the line segment from A to B, in other words all points on the shortest path from A to B. In taxicab geometry, there are many shortest paths from A to B, and
is the line segment from A to B, in other words all points on the shortest path from A to B. In taxicab geometry, there are many shortest paths from A to B, and  is the rectangle with A and B at diametrically opposed corners.
is the rectangle with A and B at diametrically opposed corners.
Snapshot 4 shows a taxicab hyperbola in which two entire quarter-planes of points satisfy the relationship  .
.
Note: Due to the different distance measures, for certain included values of  , the locus of points satisfying the definition of a Euclidean hyperbola is empty, causing the Euclidean hyperbola to "disappear".
, the locus of points satisfying the definition of a Euclidean hyperbola is empty, causing the Euclidean hyperbola to "disappear".
Based on: Eugene Krause, Taxicab Geometry: An Adventure in Non-Euclidean Geometry, Mineola, NY: Dover Publications, 1987.
Permanent Citation