Tempered Fractionally Differenced White Noise

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
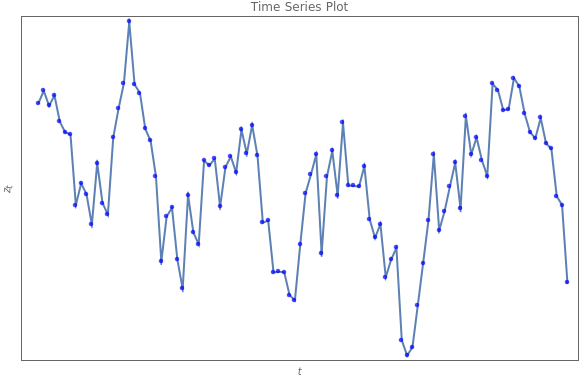
Tempered fractionally differenced (TFD) white noise 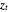 (
(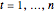 ) can be defined using the backshift operator
) can be defined using the backshift operator  in the relation
in the relation 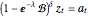 , where
, where 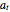 is Gaussian white noise,
is Gaussian white noise, 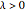 ,
, 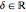 and
and  is the series length. In this Demonstration, we consider the ranges of values:
is the series length. In this Demonstration, we consider the ranges of values:  ,
, 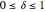 ,
, 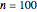 and
and 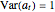 . This Demonstration explores the dependence on
. This Demonstration explores the dependence on 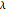 and
and  .
.
Contributed by: Ian McLeod, Mark Meerschaert and Farzad Sabzikar (September 2016)
(Western University, Michigan State University, Iowa State University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The selected range for the tempering parameter 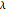 ,
, 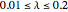 , and the differencing parameter
, and the differencing parameter  ,
, 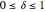 , were chosen to exhibit a wide variety of time series behavior. When
, were chosen to exhibit a wide variety of time series behavior. When 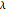 is large or
is large or  is close to zero, they are almost independent. When
is close to zero, they are almost independent. When 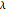 is not too large and
is not too large and  is not too small, there is a moderately strong dependence that can serve to model turbulent flow.
is not too small, there is a moderately strong dependence that can serve to model turbulent flow.
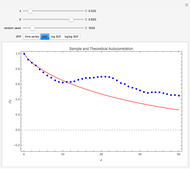
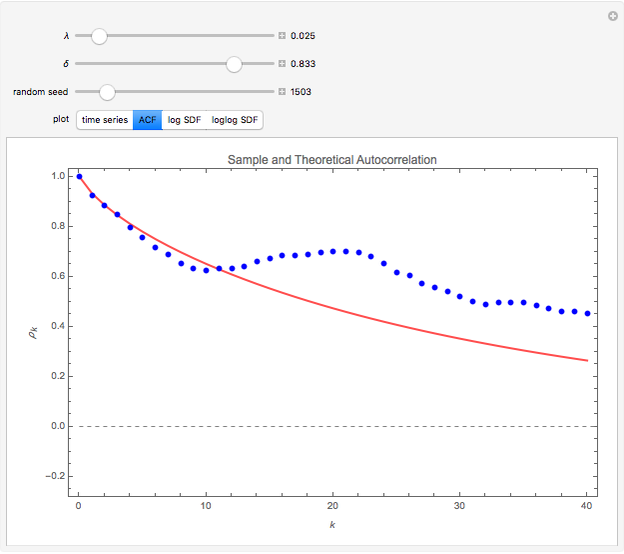
Snapshot 1: The sample and theoretical autocorrelations reveal the true structure and its estimate from the data. When the true dependence is strong, as in the case where 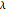 is small and
is small and  is not small, the sample estimates are not accurate and have large biases even in quite large samples. Due to this strong dependence, many spurious patterns in the sample autocorrelations may be generated. For example, setting "random seed" to 185 with
is not small, the sample estimates are not accurate and have large biases even in quite large samples. Due to this strong dependence, many spurious patterns in the sample autocorrelations may be generated. For example, setting "random seed" to 185 with 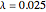 and
and 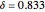 generates a spurious apparently periodic autocorrelation plot.
generates a spurious apparently periodic autocorrelation plot.
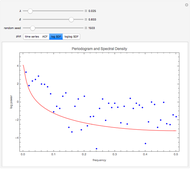
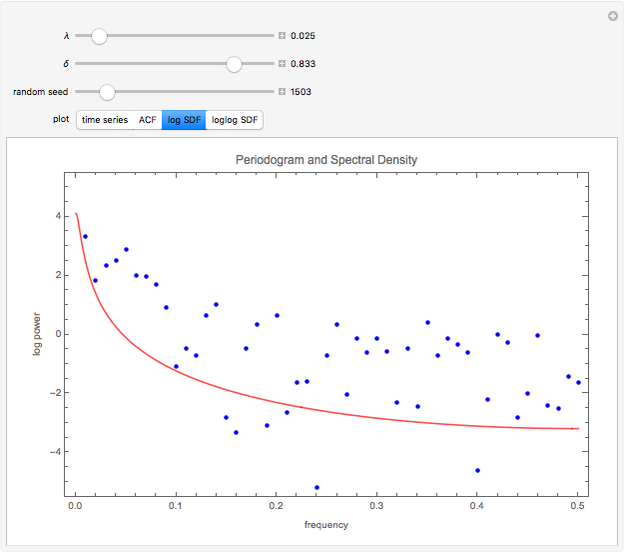
Snapshot 2: Log spectrum is plotted with the sample periodogram. The sample periodogram points scatter about the underlying theoretical value more randomly, illustrating that there is less bias than with the sample autocorrelation.
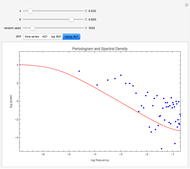
Snapshot 3: Log spectrum versus log frequency is plotted. The lowest frequency is chosen to illustrate that the TFD process has a bounded spectrum near the origin but obeys a power-law decay for intermediate frequencies.
The TFD model was suggested for turbulent flow in [1] and its extension to a more general family of models, denoted by 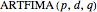 is discussed in [1] and [2]. This model is an extension to the FARIMA process.
is discussed in [1] and [2]. This model is an extension to the FARIMA process.
References
[1] M. M. Meerschaert, F. Sabzikar, M. S. Phanikumar and A. Zeleke, "Tempered Fractional Time Series Model for Turbulence in Geophysical Flows," Journal of Statistical Mechanics: Theory and Experiment, 9, 2014 P09023. stacks.iop.org/1742-5468/2014/i=9/a=P09023.
[2] A. I. McLeod, M. M. Meerschaert and F. Sabzikar, "Tempered Fractional Time Series," working paper, 2016.
Permanent Citation