Mathematica MathWorld Wolfram Science More »

Aliasing in Time Series Analysis


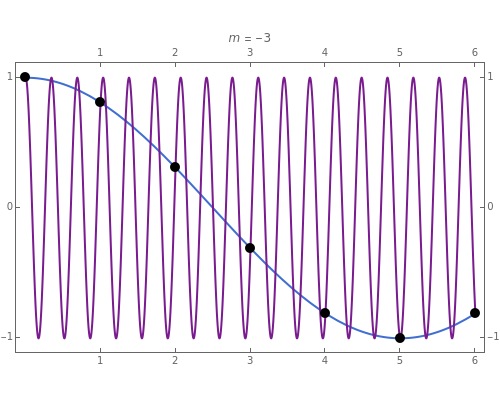
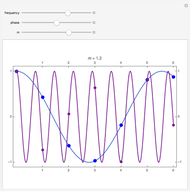
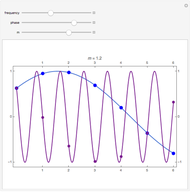
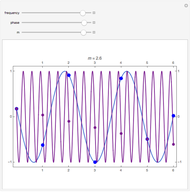
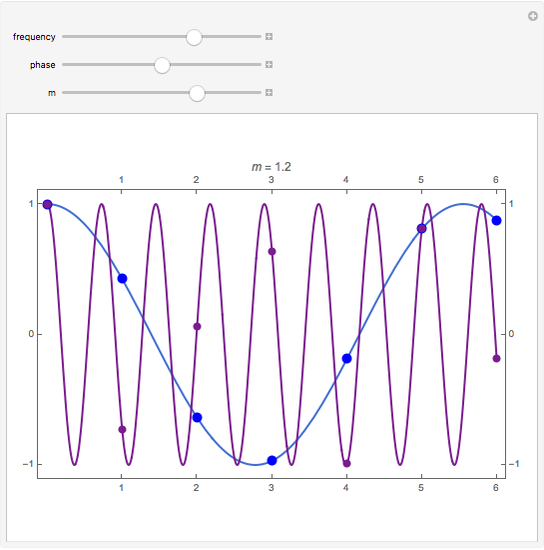
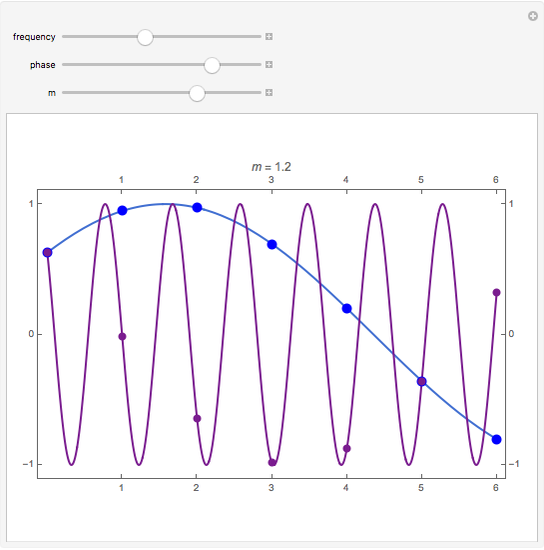
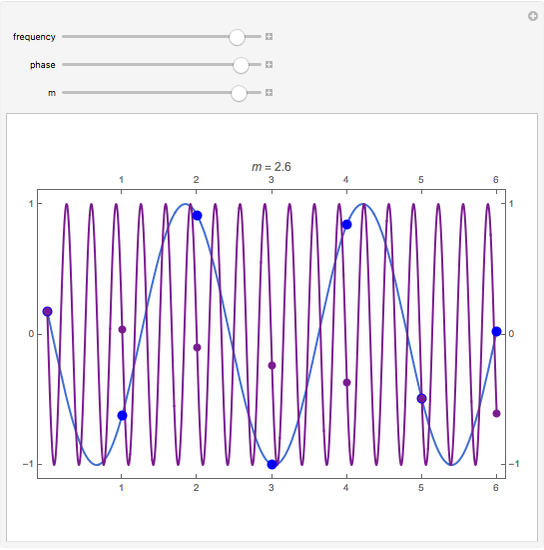
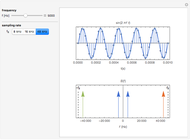
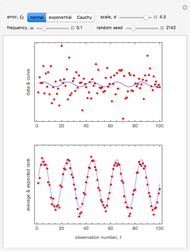
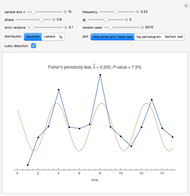
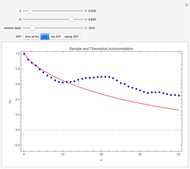
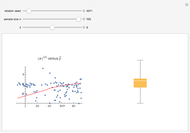
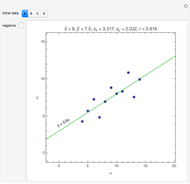
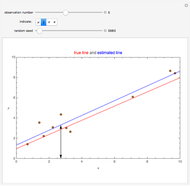
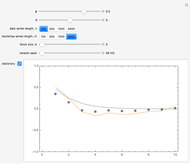
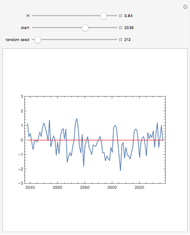
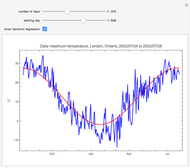
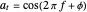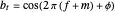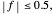
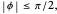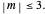	The relationship between two sinusoidal signals and is shown for and The signals are assumed to be observed at times 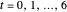and the observed points are indicated. When 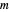is an integer the points on the curve coincide and the signals are said to be aliased. Considering all frequencies in the range 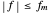, the largest value of 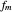so that all signals may be identified from the observed points is called the Nyquist frequency. It is well known that .


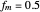	Contributed by: Ian McLeod

The spectral density function for a stationary time series

with autocovariance function

can also be written as

The sdf can be interpreted as the amount of variability accounted for by a sinusoid with frequency

Let

. Then we can write

where

is an integer and

. Then we see that

. Consequently all such frequencies

are said to be aliased with

. The highest frequency that can be represented in a discrete time series sampled at times

is 0.5 and is known as the Nyquist frequency. More generally, if the time interval between observations is Δ then the Nyquist frequency is Δ/2.

Contributed by: Ian McLeod

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom