The Traveling Salesman Problem 2: 2-opt Removal of Intersections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
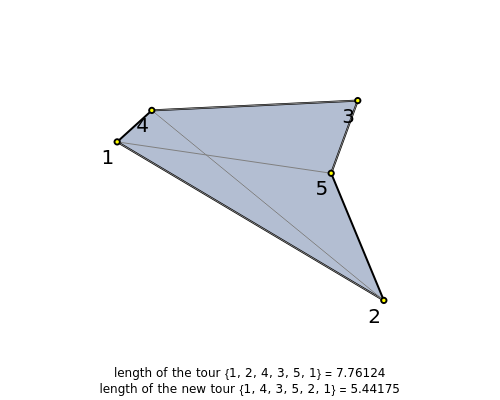
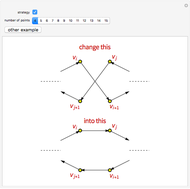
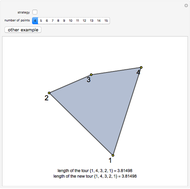
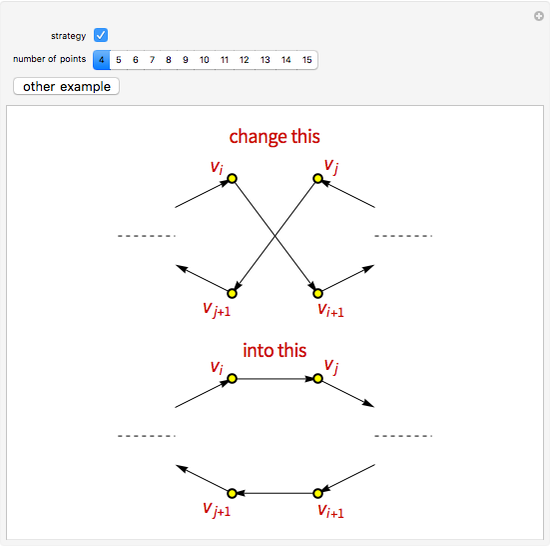
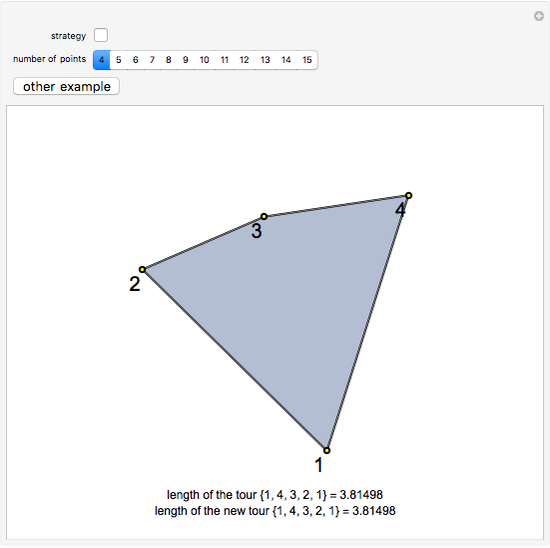
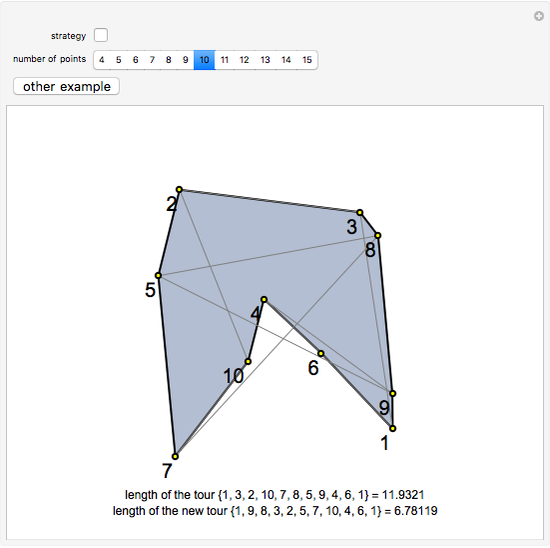
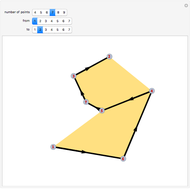
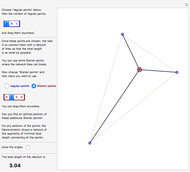
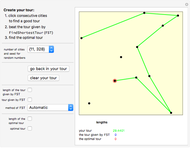
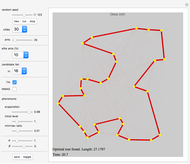
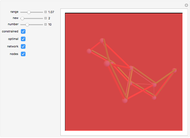
The traveling salesman problem (TSP) is the most famous combinatorial optimization problem. Its task is to find a tour through a set of vertices in the plane with the shortest possible total length. This Demonstration explores a method that helps in attaining the optimal minimum. It is based on the removal of intersections in a path to decrease its length, relying on the following fact: given 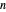 points on the plane, no three of which are collinear, there exists a closed path with no self-intersections having those points as vertices of minimal length. This method is called 2-opt and was proposed in 1958 as a way to solve the TSP. Although 2-opt does not give the optimum path, it often improves a given path. This Demonstration generates a random path and applies the method repeatedly to it, comparing the initial and final lengths obtained.
points on the plane, no three of which are collinear, there exists a closed path with no self-intersections having those points as vertices of minimal length. This method is called 2-opt and was proposed in 1958 as a way to solve the TSP. Although 2-opt does not give the optimum path, it often improves a given path. This Demonstration generates a random path and applies the method repeatedly to it, comparing the initial and final lengths obtained.
Contributed by: Jaime Rangel-Mondragon (July 2012)
Open content licensed under CC BY-NC-SA
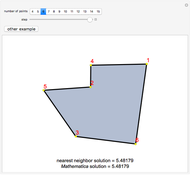
Snapshots
Details
Reference
[1] E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan, and D. B. Shmoys, eds., The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization, New York: John Wiley & Sons, 1985.
Permanent Citation