Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

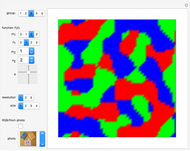
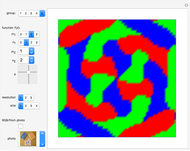
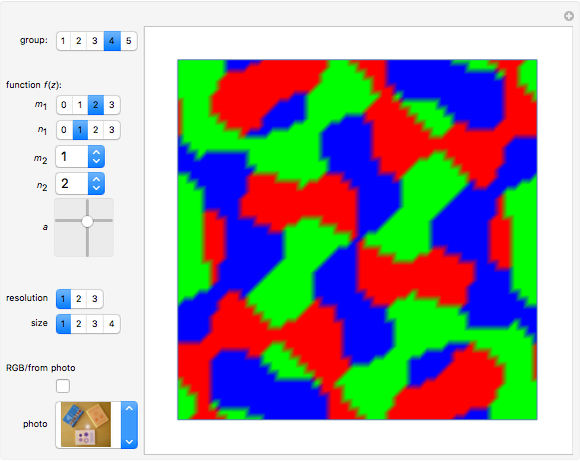
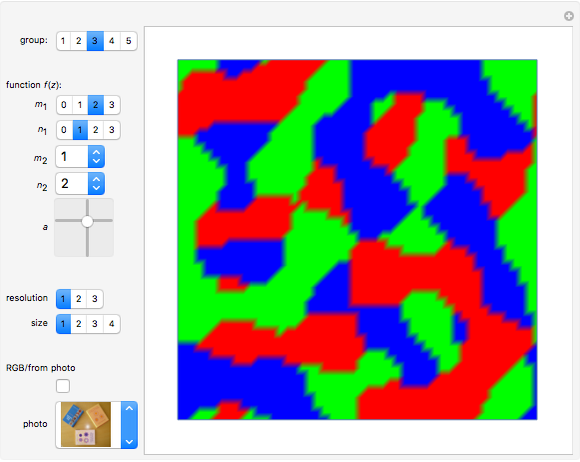
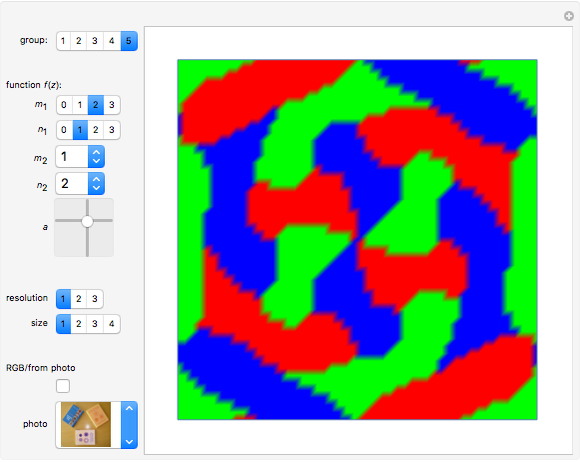
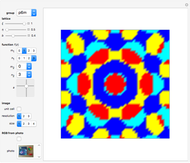
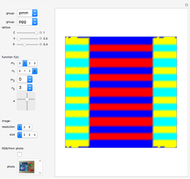
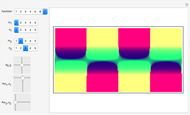
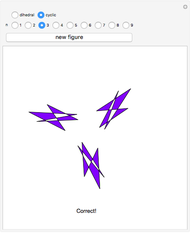
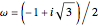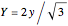Threefold Color-Turning Wallpaper Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration illustrates threefold color-turning wallpaper functions using complex functions in Fourier series of the form 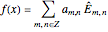, where are color-turning waves, and are called lattice waves.

[more]

The hexagonal lattice has basis vectors , , and the lattice coordinates are , .

The Fourier series are actually truncated to two terms: .

[less]

Contributed by: Izidor Hafner (April 2016)
Based on work by: Frank A. Farris
Open content licensed under CC BY-NC-SA

Snapshots

Details

The term "color-turning" refers to an -fold rotational symmetry of a figure, in which each successive image is colored differently [1].

We use the following recipes [1, pp. 131–140].

Reference

[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send