Tours through a Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
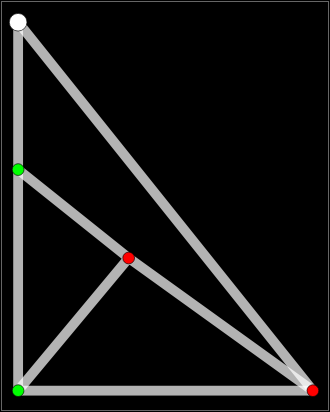
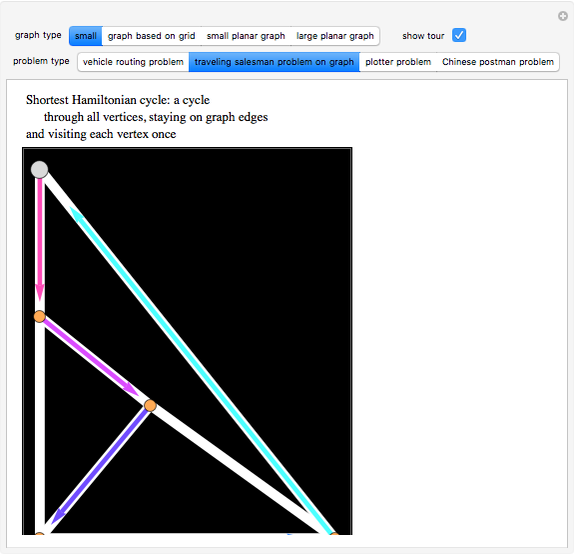
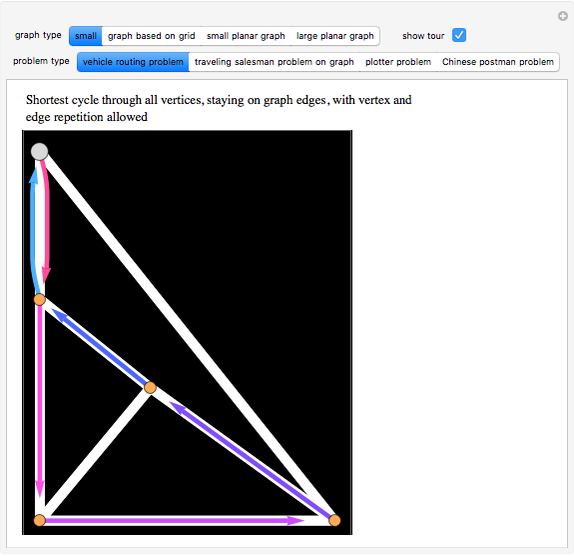
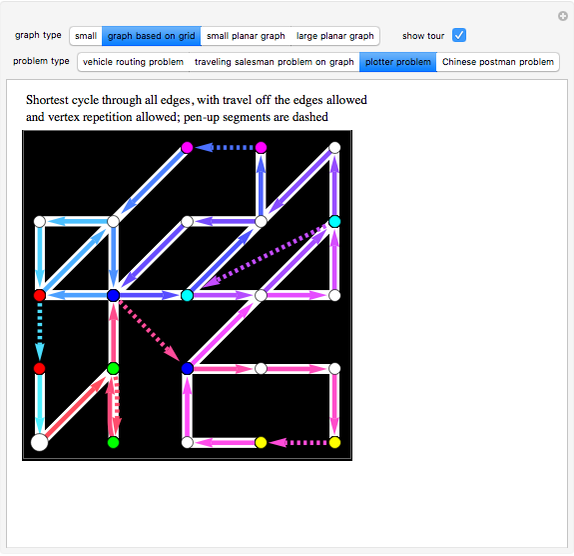
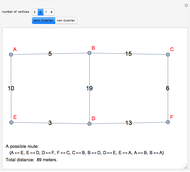
If we think of a graph as a road system, there are many types of optimal tours through the system that one might seek. This Demonstration shows four such tours, which can be found by various optimization methods. The starting point is shown as a larger gray disk.
[more]
Contributed by: Stan Wagon (July 2012)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For graphs of modest size, the method of integer linear programming can be used to solve the routing problem and the traveling salesman problem. The other two problems can be solved even for graphs of very large size by using the blossom algorithm for finding a perfect matching of minimal weight.
For the plotter problem, we form the complete graph whose vertices are all odd-degree vertices, with weights being the straight-line distance between the vertices. Then a minimal-weight perfect matching of this graph tells us which edges can be added so that the resulting graph (possibly with multiple edges) has only vertices of even degree. An Eulerian tour of the resulting graph gives the optimal plotter path, since the pen-up distance is minimized.
For the Chinese postman problem, one takes a similar approach, but the weight of an edge joining two odd-degree vertices is taken to be the length of the shortest path between them in the original network. Again, the blossom algorithm can find a minimal perfect matching, and the resulting even-degree graph is Eulerian. We find an Eulerian cycle and then replace each non-edge by the corresponding shortest path in the original network.
Permanent Citation
"Tours through a Graph"
http://demonstrations.wolfram.com/ToursThroughAGraph/
Wolfram Demonstrations Project
Published: July 2 2012