Trajectory of a Bomb

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
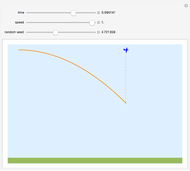
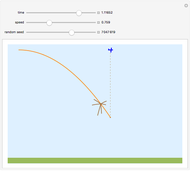
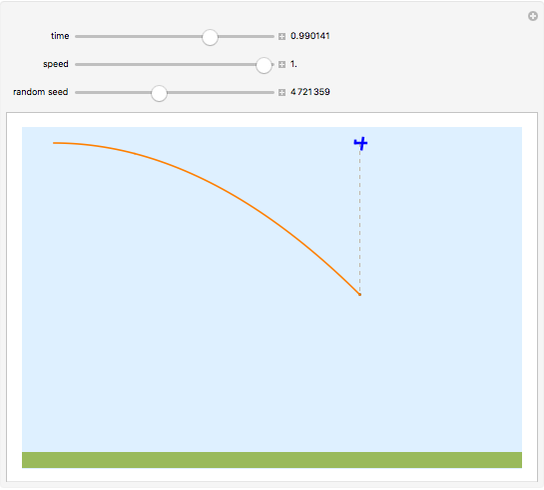
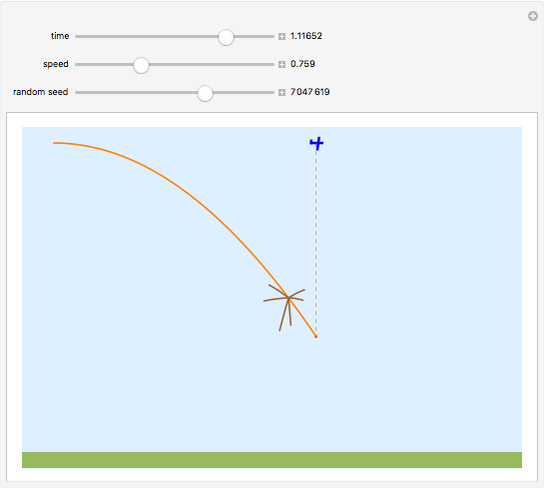
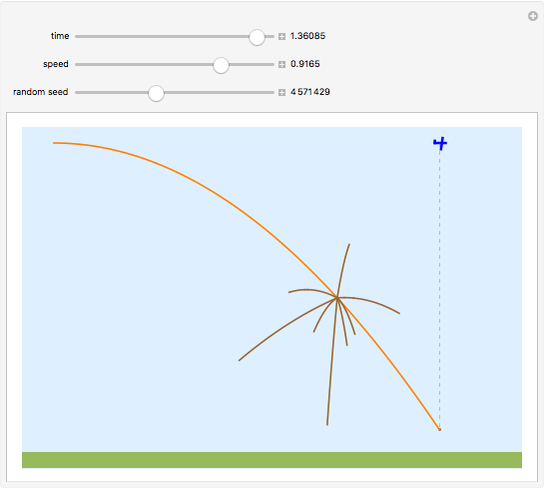
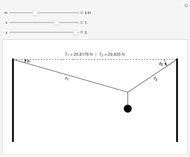
When a bomb is released from an airplane, it follows a parabolic trajectory with a horizontal speed equal to that of the airplane. The bomb falls directly below the airplane (dashed line). If the bomb explodes at some height above the ground, the center of mass of the fragments follows the original parabolic trajectory (orange curve). The momentum is conserved; that is, the vector sum of the products of the masses and the velocity for each fragment immediately before the explosion is equal to the momentum an instant after the explosion.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Mathematically, the conservation of momentum can be expressed as 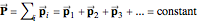 .
.
The assumption here is that gravity is parallel down and constant. Actually gravity is an central field and varies inversely with the square of the distance. In that case the trajectory follows an elliptical path.
Permanent Citation