Wolfram Demonstrations Project

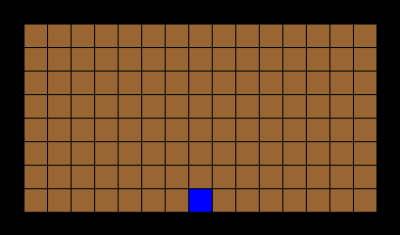
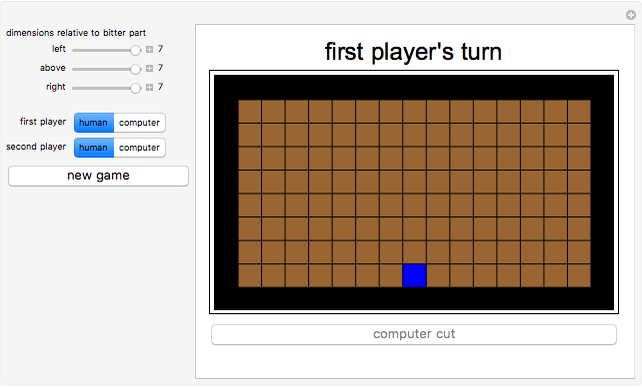
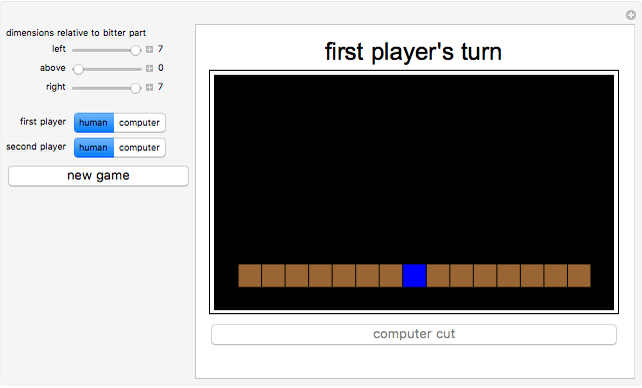
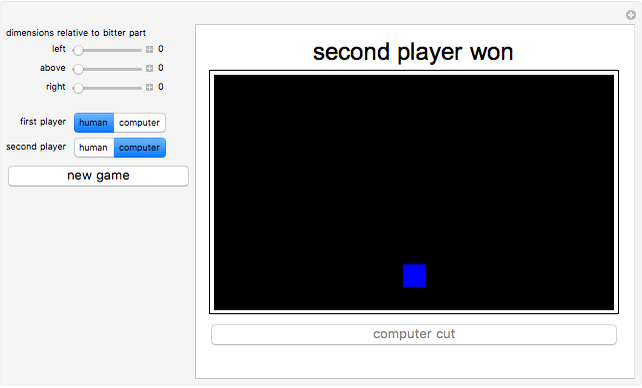
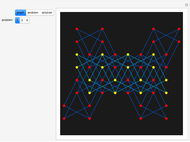
In a piece of chocolate, the brown parts are sweet and the blue part is very bitter. This game is played by two players taking turns. Each player breaks the chocolate (in a straight line along the grooves) and eats the piece that is broken off. The player that leaves the opponent with the single bitter part is the winner.

To make a move as a human, click a line. To make the computer move, click the button "computer cut".

Contributed by: Shunsuke Nakamura and Ryohei Miyadera

Slider Zoom

You can cut the chocolate to the left, right, or above the bitter square. The triple

gives the signed distances from this square in these directions.

We define two important states:

states, from which we can force a win as long as we play correctly at every stage, and

states, from which we will lose however well we play if our opponent plays correctly.

One of the most important tasks of chocolate games is to find all the

and

states of a game. Usually the number of

states is small.

In this chocolate game it is easy to find

states, since there is a formula for them:

1. The position

is an

state if and only if

, where ⊕ is the bitwise exclusive or operation (BitXor in Mathematica).
For a proof, see [1].

Once we know the formula for

states, the strategy to win is clear. Suppose that you have a

state; you can choose a move that leads to an

state. After that, any move by your opponent leads to a

state, and you can always move to an

state. Finally you reach

If you have to play with an

state, you can only win if your opponent makes a mistake.

This chocolate problem is presented in [1]. For the other chocolate games by the authors of this Demonstration, see [2], [3], [4], and [5].

References

[1] A. C. Robin, "A Poisoned Chocolate Problem," The Mathematical Gazette, 73(466), 1989 pp. 341–343. (An answer to the problem is in 74(468), 1990, pp. 171–173.)

[2] M. Naito, T. Yamauchi, H. Matsui, T. Inoue, Y. Tomari, K. Nishimura, T. Nakaoka, D. Minematsu, and R. Miyadera, "Combinatorial Games and Beautiful Graphs Produced by Them," Visual Mathematics, 11(3), 2009. www.mi.sanu.ac.rs/vismath/miyaderasept2009/index.html.

[3] R. Miyadera, S. Nakamura, and R. Hanafusa, "New Chocolate Games: Variants of the Game of Nim," Proceedings of the Annual International Conference on Computational Mathematics, Computational Geometry, and Statistics (CMCGS12), Singapore, 2012 pp. 122, 128.

[4] R. Miyadera, S. Nakamura, and R. Hanafusa, "New Chocolate Games," GSTF Journal of Mathematics, Statistics and Operations Research, 1(1), 2012 pp. 122, 128.

[5] T. Yamauchi, T. Inoue, and Y. Tomari, "Variants of the Game of Nim that Have Inequalities as Conditions," Rose–Hulman Undergraduate Mathematics Journal, 10(2), 2009. www.rose-hulman.edu/mathjournal/archives/2009/vol10-n2/paper12/v10n2-12pd.pdf.